Hostname: page-component-f554764f5-nqxm9 Total loading time: 0 Render date: 2025-04-23T02:23:54.343Z Has data issue: false hasContentIssue false
  • English
  • Français

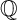ON THE ANTI-CANONICAL GEOMETRY OF WEAK $\mathbb {Q}$-FANO THREEFOLDS, III

Part of: Cycles and subschemes Surfaces and higher-dimensional varieties Birational geometry

Published online by Cambridge University Press:  22 August 2023

CHEN JIANG Open the ORCID record for CHEN JIANG [Opens in a new window]  and
YU ZOU Open the ORCID record for YU ZOU [Opens in a new window]
CHEN JIANG
Affiliation:
Shanghai Center for Mathematical Sciences and School of Mathematical Sciences Fudan University Shanghai 200438 China [email protected]
YU ZOU*
Affiliation:
Yau Mathematical Sciences Center Tsinghua University Beijing 100084 China
*
[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a terminal weak 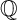${\mathbb {Q}}$-Fano threefold X, we show that the mth anti-canonical map defined by 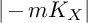$|-mK_X|$ is birational for all 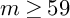$m\geq 59$.

MSC classification

Primary: 14J45: Fano varieties
Secondary: 14J30: $3$-folds 14C20: Divisors, linear systems, invertible sheaves 14E05: Rational and birational maps
Type
Article
Information
Nagoya Mathematical Journal , Volume 253 , March 2024 , pp. 23 - 47
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Jiang was supported by the National Natural Science Foundation of China for Innovative Research Groups (Grant No. 12121001) and the National Key Research and Development Program of China (Grant No. 2020YFA0713200). Jiang is a member of LMNS, Fudan University.

References

Birkar, C., Anti-pluricanonical systems on Fano varieties , Ann. Math. 190 (2019), 345–463.CrossRefGoogle Scholar
Chen, J. A. and Chen, M., An optimal boundedness on weak $\mathbb{Q}$ -Fano $3$ -folds , Adv. Math. 219 (2008), 2086–2104.CrossRefGoogle Scholar
Chen, J.-J., Chen, J. A., Chen, M., and Jiang, Z., On quint-canonical birationality of irregular threefolds , Proc. Lond. Math. Soc. (3) 122 (2021), 234–258.CrossRefGoogle Scholar
Chen, M., On anti-pluricanonical systems of $\mathbb{Q}$ -Fano $3$ -folds , Sci China Math. 54 (2011), 1547–1560.CrossRefGoogle Scholar
Chen, M. and Jiang, C., On the anti-canonical geometry of $\mathbb{Q}$ -Fano threefolds , J. Differ. Geom. 104 (2016), 59–109.CrossRefGoogle Scholar
Chen, M. and Jiang, C., On the anti-canonical geometry of weak $\mathbb{Q}$ -Fano threefolds II , Ann. Inst. Fourier (Grenoble) 70 (2020), 2473–2542.CrossRefGoogle Scholar
Dolgachev, I. V., Classical Algebraic Geometry: A Modern View, Cambridge University Press, Cambridge, 2012.CrossRefGoogle Scholar
Iano-Fletcher, A. R., “Working with weighted complete intersections” in Explicit Birational Geometry of 3-Folds, London Math. Soc. Lecture Note Ser. 281, Cambridge Univ. Press, Cambridge, 2000, 101–173.CrossRefGoogle Scholar
Jiang, C., On birational geometry of minimal threefolds with numerically trivial canonical divisors , Math. Ann. 365 (2016), 49–76.CrossRefGoogle Scholar
Jiang, C., “Characterizing terminal Fano threefolds with the smallest anti-canonical volume” in Birational Geometry, Kähler–Einstein Metrics and Degenerations, Moscow, Shanghai and Pohang, June–November 2019, Springer Proc. Math. Stat. 409, Springer, Cham, 2023, 355–362.CrossRefGoogle Scholar
Jiang, C., Characterizing terminal Fano threefolds with the smallest anti-canonical volume, II, contributing to the special volume in honor of Professor Shokurov’s seventieth birthday, preprint, arXiv:2207.03832v1 Google Scholar
Jiang, C. and Zou, Y., An effective upper bound for anti-canonical volumes of canonical $\mathbb{Q}$ -Fano three-folds , Int. Math. Res. Not. 2023, 9298–9318. https://doi.org/10.1093/imrn/rnac100.CrossRefGoogle Scholar
Kollár, J., Miyaoka, Y., Mori, S., and Takagi, H., Boundedness of canonical $\mathbb{Q}$ -Fano $3$ -folds , Proc. Japan Acad. Ser. A Math. Sci. 76 (2000), 73–77.CrossRefGoogle Scholar
Kollár, J. and Mori, S., Birational Geometry of Algebraic Varieties, Cambridge Tracts in Math. 134, Cambridge University Press, Cambridge, 1998.CrossRefGoogle Scholar
Miyanishi, M. and Zhang, D.-Q., Gorenstein log del Pezzo surfaces of rank one , J. Algebra 118 (1988), 63–84.CrossRefGoogle Scholar
Prokhorov, Y. G., The degree of Fano threefolds with canonical Gorenstein singularities . Mat. Sb. 196 (2005), 81–122; translation in Sb. Math. 196 (2005), 77–114.Google Scholar
Prokhorov, Y. G., The degree of $\mathbb{Q}$ -Fano threefolds , Mat. Sb. 198 (2007), 153–174; translation in Sb. Math. 198 (2007), 1683–1702.Google Scholar
Prokhorov, Y. G., $\mathbb{Q}$ -Fano threefolds of large Fano index, I , Doc. Math. 15 (2010), 843–872.CrossRefGoogle Scholar
Prokhorov, Y. G., On Fano threefolds of large Fano index and large degree , Mat. Sb. 204 (2013), 43–78; translation in Sb. Math. 204 (2013), 347–382.Google Scholar
Reid, M., “Young person’s guide to canonical singularities” in Algebraic Geometry, Bowdoin, 1985 (Brunswick, Maine, 1985), Proc. Sympos. Pure Math. 46(1), Amer. Math. Soc., Providence, RI, 1987, 345–414.Google Scholar