Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Watanabe, Toshiro
1993.
Oscillation of modes of some semi-stable Lévy processes.
Nagoya Mathematical Journal,
Vol. 132,
Issue. ,
p.
141.
Yamazato, M.
1996.
On Strongly Unimodal Infinitely Divisible Distributions of Class CME.
Theory of Probability & Its Applications,
Vol. 40,
Issue. 3,
p.
518.
Tomisaki, Matsuyo
and
Yamazato, Makoto
1998.
Limit theorems for hitting times of 1-dimensional generalized diffusions.
Nagoya Mathematical Journal,
Vol. 152,
Issue. ,
p.
1.


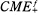 distribution if there are an increasing (in the strict sense) sequence of positive real numbers
distribution if there are an increasing (in the strict sense) sequence of positive real numbers 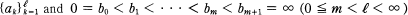 such that, for each
such that, for each 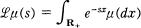 of
of