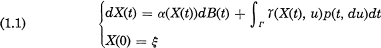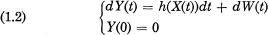Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kushner, Harold J.
and
Runggaldier, W.
1986.
Analysis and Optimization of Systems.
Vol. 83,
Issue. ,
p.
471.
Kushner, Harold J.
and
Runggaldier, W.
1987.
Nearly Optimal State Feedback Controls for Stochastic Systems with Wideband Noise Disturbances.
SIAM Journal on Control and Optimization,
Vol. 25,
Issue. 2,
p.
298.
EL Karoui, Nicole
1987.
Stochastic Differential Systems.
Vol. 96,
Issue. ,
p.
272.
Chitashvili, R. J.
and
Mania, M. G.
1987.
Optimal locally absolutely continuous change of measure. finite set of decisions. part ii:optimization problems.
Stochastics,
Vol. 21,
Issue. 3,
p.
187.
Nicole el, Karoui
Du'hŪŪ, Nguyen
and
Monique, Jeanblanc-Picqué
1987.
Compactification methods in the control of degenerate diffusions: existence of an optimal control.
Stochastics,
Vol. 20,
Issue. 3,
p.
169.
Borkar, Vivek S
1987.
Control of a partially observed diffusion up to an exit time.
Systems & Control Letters,
Vol. 8,
Issue. 5,
p.
429.
Chitashvili, R. J.
and
Mania, M. G.
1987.
Stochastic Differential Systems.
Vol. 96,
Issue. ,
p.
253.
Chitashvili, R. J.
and
Mania, M. G.
1987.
Optimal locally absolutely continuous change of measure. finite set of decisions. part i.
Stochastics,
Vol. 21,
Issue. 2,
p.
131.
Kushner, Harold J.
1988.
Stochastic Differential Systems, Stochastic Control Theory and Applications.
Vol. 10,
Issue. ,
p.
255.
El Karoui, Nicole
Nguyen, Du′ Huù
and
Jeanblanc-Picqué, Monique
1988.
Existence of an Optimal Markovian Filter for the Control under Partial Observations.
SIAM Journal on Control and Optimization,
Vol. 26,
Issue. 5,
p.
1025.
Borkar, Vivek S.
1988.
The probabilistic structure of controlled diffusion processes.
Acta Applicandae Mathematicae,
Vol. 11,
Issue. 1,
p.
19.
Hijab, Omar
1989.
partially observed control of markov processes, I.
Stochastics and Stochastic Reports,
Vol. 28,
Issue. 2,
p.
123.
Lions, P. L.
1989.
Stochastic Partial Differential Equations and Applications II.
Vol. 1390,
Issue. ,
p.
147.
Cohen, Robert
and
Mazziotto, Gérald
1989.
Stochastic continuous control of partially observed systems via impulse control problems.
Stochastics and Stochastic Reports,
Vol. 26,
Issue. 2,
p.
101.
Nagase, Noriaki
and
Nisio, Makiko
1990.
Optimal Controls for Stochastic Partial Differential Equations.
SIAM Journal on Control and Optimization,
Vol. 28,
Issue. 1,
p.
186.
Zhang, Qing
1990.
Controlled partially observed diffusions with correlated noise.
Applied Mathematics & Optimization,
Vol. 22,
Issue. 1,
p.
265.
Kushner, Harold J.
1990.
Numerical Methods for Stochastic Control Problems in Continuous Time.
SIAM Journal on Control and Optimization,
Vol. 28,
Issue. 5,
p.
999.
Bensoussan, A.
and
Nisio, M.
1990.
Nonlinear semigroup arising in the control of diffusions with partial observation.
Stochastics and Stochastic Reports,
Vol. 30,
Issue. 1,
p.
1.
El Karoui, N.
and
Jeanblac-Picqué, M.
1991.
Martingale measures and partially observable diffusions.
Stochastic Analysis and Applications,
Vol. 9,
Issue. 2,
p.
147.
Hijab, Omar
1992.
Partially observed control of Markov processes, IV.
Journal of Functional Analysis,
Vol. 109,
Issue. 2,
p.
215.