Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T23:36:16.752Z Has data issue: false hasContentIssue false
  • English
  • Français

On stochastic optimal control laws

Published online by Cambridge University Press:  22 January 2016

Makiko Nisio
Makiko Nisio*
Affiliation:
Kobe University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let us begin by recalling the existence of optimal controls for a class of stochastic differential equations

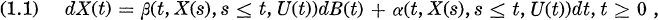
with given initial condition X(0) = x, where B is an n-dimensional Brownian motion and the control U is a stochastic process. As admissible controls, let us allow all non-anticipative process U(t) = (U1(t),…Um(t)) ∈ Γ where Γ is a compact subset of Rm. We call Γ a control region. Assume that the matrix valued functional β and the n-vector valued α satisfy a Lipscitz condition in X and some growth condition. Then we have a unique solution Xu for an admissible control U.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 52 , December 1973 , pp. 1 - 30
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1973

References

[1] Beneš, V. E., Existence of optimal strategies based on specified informations, for a class of stochastic decision problems, SIAM J. control, 8 (1970), 179–188.Google Scholar
[2] Beneš, V. E., Existence of optimal stochastic control laws, SIAM J. control, 9 (1971), 446–472.Google Scholar
[3] Fleming, W. H., Some Markovian optimization problems, J. Math. & Mech., 12 (1963), 131–140.Google Scholar
[4] Fleming, W. H. & Nisio, M., On the existence of optimal stochastic controls, J. Math. & Mech., 15 (1966), 779–794.Google Scholar
[5] Fujisaki, M., Kallianpur, G. & Kunita, H., Stochastic differential equations for the non-linear filtering problem, Osaka J. Math., 9 (1972), 19–40.Google Scholar
[6] Itô, K., On a formula concerning stochastic differentials, Nagoya Math. J., 3 (1951), 55–65.CrossRefGoogle Scholar
[7] Krylov, N. V., On the stochastic integral of Itô, Th. Prob. Appl., 14 (1969), 330–336.CrossRefGoogle Scholar
[8] Krylov, N. V., On an inequality in the theory of stochastic integrals, T. V., 16 (1971), 446–457.Google Scholar
[9] Krylov, N. V., On the control of diffusion type processes, 2nd Japan-USSR Symp. Proba. Th. (1972).Google Scholar
[10] Kunita, H. & Watanabe, S., On square integrable martingales, Nagoya Math. J., 30 (1967), 209–245.CrossRefGoogle Scholar
[11] McKean, H. P., Stochastic Integrals. Acad. Press, 1969.Google Scholar