Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Denzel, G. E.
1966.
The hitting characteristics of a strong Markov process, with applications to continuous martingales in 𝑅ⁿ.
Bulletin of the American Mathematical Society,
Vol. 72,
Issue. 6,
p.
1026.
Denzel, Gene
1967.
The exit characteristics of Markov processes with applications to continuous martingales in Rⁿ.
Transactions of the American Mathematical Society,
Vol. 129,
Issue. 1,
p.
111.
Kazamaki, Norihiko
1968.
On the equivalence of $q$-martingales and locally $L^{p}$-integrable martingales.
Tohoku Mathematical Journal,
Vol. 20,
Issue. 3,
Kunita, Hiroshi
1969.
Absolute Continuity of Markov Processes and Generators.
Nagoya Mathematical Journal,
Vol. 36,
Issue. ,
p.
1.
Dol�ans-Dade, C.
1970.
Quelques applications de la formule de changement de variables pour les semimartingales.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 16,
Issue. 3,
p.
181.
Doléans-Dade, C.
and
Meyer, P. A.
1970.
Séminaire de Probabilités IV Université de Strasbourg.
Vol. 124,
Issue. ,
p.
77.
Kailath, T.
1970.
A further note on a general likelihood formula for random signals in Gaussian noise.
IEEE Transactions on Information Theory,
Vol. 16,
Issue. 4,
p.
393.
Kunita, Hiroshi
1970.
Stochastic Integrals Based on Martingales Taking Values in Hilbert Space.
Nagoya Mathematical Journal,
Vol. 38,
Issue. ,
p.
41.
Duncan, Tyrone E.
1970.
Likelihood functions for stochastic signals in white noise.
Information and Control,
Vol. 16,
Issue. 4,
p.
303.
Stroock, Daniel W.
and
Varadhan, S. R. S.
1971.
Diffusion processes with boundary conditions.
Communications on Pure and Applied Mathematics,
Vol. 24,
Issue. 2,
p.
147.
Meyer, Paul A.
1971.
Martingales.
Vol. 190,
Issue. ,
p.
32.
Knight, Frank B.
1971.
Martingales.
Vol. 190,
Issue. ,
p.
19.
Kailath, Thomas
1971.
Some Extensions of the Innovations Theorem*.
Bell System Technical Journal,
Vol. 50,
Issue. 4,
p.
1487.
Kunita, Hiroshi
1971.
Asymptotic behavior of the nonlinear filtering errors of Markov processes.
Journal of Multivariate Analysis,
Vol. 1,
Issue. 4,
p.
365.
Sam Lazaro, J.
and
Meyer, P. A.
1971.
M�thodes de martingales et th�orie des flots.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 18,
Issue. 2,
p.
116.
Duncan, Tyrone E.
1971.
Mutual information for stochastic differential equations.
Information and Control,
Vol. 19,
Issue. 3,
p.
265.
Wong, E.
1971.
Representation of Martingales, Quadratic Variation and Applications.
SIAM Journal on Control,
Vol. 9,
Issue. 4,
p.
621.
Snyder, D.
1972.
Filtering and detection for doubly stochastic Poisson processes.
IEEE Transactions on Information Theory,
Vol. 18,
Issue. 1,
p.
91.
Duncan, T. E.
1972.
Stability of Stochastic Dynamical Systems.
Vol. 294,
Issue. ,
p.
85.
Beutler, F.
1972.
Review of 'Stochastic Processes in Information and Communication Systems' (Wong, E.; 1971).
IEEE Transactions on Information Theory,
Vol. 18,
Issue. 6,
p.
827.


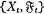 be a square integrable martingale on a probability space
be a square integrable martingale on a probability space