Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
De Koninck, J. M.
Kátai, I.
and
Mercier, A.
1992.
On the Normal Growth of Prime Factors of Integers.
Canadian Journal of Mathematics,
Vol. 44,
Issue. 6,
p.
1121.
Stef, André
and
Tenenbaum, Gérald
1998.
Analytic and Elementary Number Theory.
Vol. 1,
Issue. ,
p.
167.
Sándor, J.
and
Crstici, B.
2004.
Handbook of Number Theory II.
p.
329.
Ford, Kevin
and
Gabdullin, Mikhail
2021.
Sets whose differences avoid squares modulo 𝑚.
Proceedings of the American Mathematical Society,
Vol. 149,
Issue. 9,
p.
3669.
Bettin, Sandro
Koukoulopoulos, Dimitris
and
Sanna, Carlo
2021.
A note on the natural density of product sets.
Bulletin of the London Mathematical Society,
Vol. 53,
Issue. 5,
p.
1407.


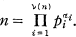 A well known theorem of Hardy and Ramanujan states:
A well known theorem of Hardy and Ramanujan states: