Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tanigawa, Yoshio
and
Ishikawa, Hirofumi
1988.
The dimension formula of the space of cusp forms of weight one for Γ0(p).
Nagoya Mathematical Journal,
Vol. 111,
Issue. ,
p.
115.
Akiyama, Shigeki
1988.
Selberg trace formula for odd weight, I.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 64,
Issue. 9,
Hiramatsu, Toyokazu
1989.
Automorphic Forms and Geometry of Arithmetic Varieties.
p.
287.
Christian, Ulrich
1991.
Über ``Primzahlsätze'' für hyperbolische Klassen und die Konvergenzabszisse der logarithmischen Ableitung einer Selberg'schen Zetafunktion für elliptische Modulgruppen.
Tohoku Mathematical Journal,
Vol. 43,
Issue. 3,


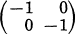 . Let
. Let 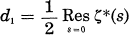 ,
,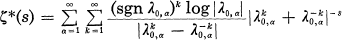 .
.