Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T23:48:03.690Z Has data issue: false hasContentIssue false
  • English
  • Français

On some dimension formula for automorphic forms of weight one I

Published online by Cambridge University Press:  22 January 2016

Toyokazu Hiramatsu
Toyokazu Hiramatsu*
Affiliation:
Department of Mathematics, Kobe University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Γ be a fuchsian group of the first kind not containing the element 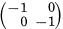. We shall denote by d0 the number of linearly independent automorphic forms of weight 1 for Γ. It would be interesting to have a certain formula for d0. But, Hejhal said in his Lecture Notes 548, it is impossible to calculate d0 using only the basic algebraic properties of Γ. On the other hand, Serre has given such a formula of d0 recently in a paper delivered at the Durham symposium ([7]). His formula is closely connected with 2-dimensional Galois representations.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 85 , March 1982 , pp. 213 - 221
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1982

References

[ 1 ] Hiramatsu, T., Eichler classes attached to automorphic forms of dimension -1, Osaka J. Math., 3 (1966), 39–48.Google Scholar
[ 2 ] Hiramatsu, T., On some dimension formula for automorphic forms of weight one II, to appear.Google Scholar
[ 3 ] Huber, H., Zur analytichen Theorie hyperbolischer Raumformen und Bewegungsgruppen, Math. Annalen, 138 (1959), 1–26.CrossRefGoogle Scholar
[ 4 ] Kuga, M., Functional analysis in weakly symmetric Riemannian spaces and its applications, (in Japanese), Sugaku, 9 (1957), 166–185.Google Scholar
[ 5 ] Kuga, M., On a uniformity of distribution of 0-cycles and the eigenvalues of Hecke operators, II, Sci. Papers College Gen. Ed. Univ. Tokyo, 10 (1961), 171–186.Google Scholar
[ 6 ] Selberg, A., Harmonic analysis and discontinuous groups in weakly symmetric Riemannian spaces with applicationss to Dirichlet series, J. Indian Math. Soc, 20 (1956), 47–87.Google Scholar
[ 7 ] Serre, J.-P., Modular forms of weight one and Galois representations, In: Proc. Symposium on Algebraic Number Fields, 193–268. Academic Press, 1977.Google Scholar