Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Matsuzawa, Tadato
1973.
On some degenerate parabolic equations II.
Nagoya Mathematical Journal,
Vol. 52,
Issue. ,
p.
61.
Miyake, Masatake
1975.
A note on partially hypoelliptic operators.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 51,
Issue. 1,
Matsuzawa, Tadato
1975.
On a hypoelliptic boundary value problem.
Nagoya Mathematical Journal,
Vol. 59,
Issue. ,
p.
87.
Matsuzawa, Tadato
1977.
Hypoellipticity for a class of the second order partial differential equations.
Nagoya Mathematical Journal,
Vol. 66,
Issue. ,
p.
1.
Pao, C. V.
1977.
The cauchy problem of a degenerate parabolic equation.
Monatshefte f�r Mathematik,
Vol. 83,
Issue. 3,
p.
201.
Matsuzawa, T.
1978.
Construction of fundamental solutions of hypoelliptic equations by the use of a probabilistic method.
Nagoya Mathematical Journal,
Vol. 72,
Issue. ,
p.
103.
Gramchev, Todor
Popivanov, Petar
and
Yoshino, Massafumi
1996.
Critical Gevrey index for hypoellipticity of parabolic operators and Newton polygones.
Annali di Matematica Pura ed Applicata,
Vol. 170,
Issue. 1,
p.
103.
Oliaro, Alessandro
and
Popivanov, Petar
2007.
Modern Trends in Pseudo-Differential Operators.
Vol. 172,
Issue. ,
p.
135.
Arias Junior, Alexandre
and
de Lessa Victor, Bruno
2025.
The Cauchy problem for a class of linear degenerate evolution equations on the torus.
Journal of Mathematical Analysis and Applications,
Vol. 542,
Issue. 1,
p.
128751.


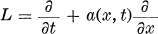 .
.