Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T22:57:35.212Z Has data issue: false hasContentIssue false
  • English
  • Français

On some class number relations for Galois extensions

Published online by Cambridge University Press:  22 January 2016

Takashi Ono
Takashi Ono*
Affiliation:
Department of Mathematics, The Johns Hopkins University, Baltimore, MD 21218, U. S. A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

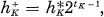Let k be an algebraic number field of finite degree over Q, the field of rationals, and K be an extension of finite degree over k. By the use of the class number of algebraic tori, we can introduce an arithmetical invariant E(K/k) for the extension K/k. When k = Q and K is quadratic over Q, the formula of Gauss on the genera of binary quadratic forms, i.e. the formula where 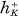= the class number of K in the narrow sense, 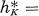the number of classes is a genus of the norm form of K/Q and tK = the number of distinct prime factors of the discriminant 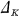of K, may be considered as an equality between E(K/Q) and other arithmetical invariants of K.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 107 , September 1987 , pp. 121 - 133
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1987

References

[C1] Chevalley, C., Sur la théorie du corps de classes dans les corps finis et les corps locaux. J. Fac. Sci. Tokyo Univ., 2 (1933), 365–476.Google Scholar
[C2] Chevalley, C., Théorie des Groupes de Lie, Tome II, Groupes algébriques, Hermann, Paris, 1951.Google Scholar
[K1] Kimura, T., Algebraic Class Number Formulae for Cyclotomic Fields, Lecture Notes, (in Japanese), Sophia Univ., Tokyo, 1985.Google Scholar
[L1] Lang, S., Algebraic Number Theory, Addison-Wesley, Reading, Mass., 1970.Google Scholar
[L2] Lang, S., Units and class groups in number theory and algebraic geometry, Bull. Am. Math. Soc, 6 (1982), 253–316.Google Scholar
[O1] Ono, T., Arithmetic of algebraic tori, Ann. of Math., 74 (1961), 101–139.Google Scholar
[O2] Ono, T., On the Tamagawa number of algebraic tori, Ann. of Math., 78 (1963), 47–73.Google Scholar
[O3] Ono, T., Arithmetic of Algebraic Groups and its Applications, Lecture Notes, Rikkyo Univ., Tokyo, 1986.Google Scholar
[S1] Shyr, J.-M., Class number formula of algebraic tori with applications to relative class numbers of certain relative quadratic extensions of algebraic number fields, Thesis, The Johns Hopkins Univ., Baltimore, Maryland, 1974.Google Scholar
[S2] Shyr, J.-M., On some class number relations of algebraic tori, Michigan Math. J., 24 (1977), 365–377.Google Scholar
[T1] Takagi, T., Lectures on Elementary Number Theory, 2nd ed. (in Japanese), Kyo-ritsu, Tokyo, 1971.Google Scholar
[W1] Washington, L., Introduction to Cyclotomic Fields, Springer New York, 1982.Google Scholar