Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T23:10:51.959Z Has data issue: false hasContentIssue false
  • English
  • Français

On singular sets of flat holomorphic mappings with isolated singularities

Published online by Cambridge University Press:  22 January 2016

Hideo Omoto
Hideo Omoto*
Affiliation:
Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [4] B. Iversen studied critical points of algebraic mappings, using algebraic-geometry methods. In particular when algebraic maps have only isolated singularities, he shows the following relation; Let V and S be compact connected non-singular algebraic varieties of dimcV = n, and dimc S = 1, respectively. Suppose f is an algebraic map of V onto S with isolated singularities. Then it follows that

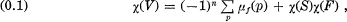
where χ denotes the Euler number, μf(p) is the Milnor number of f at the singular point p, and F is the general fiber of f : V → S.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 70 , July 1978 , pp. 47 - 80
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1978

References

[1] Borel, A. and Hirzebruch, F., Characteristic classes and homogeneous spaces I, Amer. J. Math. 80 (1958), 458–538.Google Scholar
[2] Bott, R. and Chern, S. S., Hermitian vector bundles and equidistribution of the zeros of their holomorphic sections, Acta Math. 114 (1965), 71–112.CrossRefGoogle Scholar
[3] Gunning, R. C. and Rossi, H., Analytic functions of several complex variables, Prentice-Hall, New Jersey, 1965.Google Scholar
[4] Iversen, B., Critical points of an algebraic function, Inv. Math. 18 (1971), 210–224.CrossRefGoogle Scholar
[5] Martinet, J., Sur les singularites des formes differentielles, Ann. Inst. Fourier, Grenoble 20 (1970), 95–178.Google Scholar
[6] Omoto, H., An integral formula for the Chern form of a hermitian bundles, Nagoya Math. J. 42 (1971), 135–172.CrossRefGoogle Scholar
[7] Steenrod, N., The topology of fiber bundles, Princeton Univ. Press, 1951.Google Scholar
[8] Whiteney, H., Tangents to an analytic variety, Ann. of Math. 81 (1965), 496–549.Google Scholar