Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T23:30:19.568Z Has data issue: false hasContentIssue false
  • English
  • Français

On Siegel modular forms part II

Published online by Cambridge University Press:  22 January 2016

Bernhard Runge
Bernhard Runge*
Affiliation:
Max-Planck- A rbeitsgruppe ‘Algebraische Geometrie und Zahlentheorie’Jägerstraβe 10/1110117 BerlinGermany e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

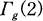In this paper we compute dimension formulas for rings of Siegel modular forms of genus g = 3. Let denote the main congruence subgroup of level two, 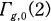the Hecke subgroup of level two and 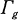the full modular group. We give the dimension formulas for genus 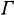g = 3 for the above mentioned groups and determine the graded ring 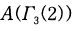of modular forms with respect to .

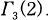Type
Research Article
Information
Nagoya Mathematical Journal , Volume 138 , June 1995 , pp. 179 - 197
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1995

References

[F] Freitag, E., Siegelsche Modulfunktionen, (Grundlehren der math. Wissenschaften, vol. 254), Springer, Berlin Heidelberg-New York, 1983.Google Scholar
[Ha] Hartshorne, R., Algebraic Geometry, Graduate Texts in Math., 52, Springer, New York-Berlin 1977.Google Scholar
[Ib1] Ibukiyama, T., On symplectic Euler factors of genus two, J. Fac. Sci. Univ. Tokyo, Sect. IA Math., 30 (1984), 587–614.Google Scholar
[Ib2] Ibukiyama, T. On Siegel modular varieties of level 3, Internat. J. Math., 2, No. 2 (1991), 17–35.CrossRefGoogle Scholar
[I1] Igusa, J., On Siegel modular forms of genus two, Amer. J. Math., 84 (1962), 175–200.CrossRefGoogle Scholar
[I2] Igusa, J., On Siegel modular forms of genus two (2), Amer J. Math., 86 (1964), 392–412.Google Scholar
[I3] Igusa, J., On the graded ring of theta-constants, Amer J. Math., 86 (1964), 219–246.Google Scholar
[I4] Igusa, J., On the graded ring of theta constants II, Amer J. Math. 88 (1966), 221–236.Google Scholar
[R] Runge, B., On Siegel modular forms, part I, J. Reine angew. Math., 436 (1993), 57–85.Google Scholar
[SM1] Salvati Manni, R., On the projective varieties associated with some subrings of the ring of Thetanullwerte, preprint 1992.Google Scholar
[SM2] Salvati Manni, R., Maps defined by Thetanullwerte, preprint 1992.Google Scholar
[Sh] Shioda, T., On the graded ring of invariants of binary octavics, Amer, J. Math., 89 (1967), 1022–1046.CrossRefGoogle Scholar
[S1] Stanley, R. P., Hilbert functions of graded algebras, Adv. in Math., 28 (1978), 57–83.Google Scholar
[S2] Stanley, R. P., Invariants of finite groups and their applications to combinatorics, Bull Amer. Math. Soc, 1, 3 (1979), 475–511.CrossRefGoogle Scholar
[T1] Tsuyumine, S., On Siegel modular forms of degree three, Amer. J. Math., 108 (1986), 755–862.Google Scholar
[T2] Tsuyumine, S., Addendum to “On Siegel domular forms of degree three”, Amer. J. Math., 108 (1986), 1001–1003.Google Scholar
[T3] Tsuyumine, S., Rings of automorphic forms which are not Cohen-Macaulay II, J. Math. Soc. Japan, 40 (1988), 369–381.Google Scholar
[T4] Tsuyumine, S., On the Graded Rings of Modular Forms in Several Variables, Adv. Stud, in Pure Math., 15, Automorphic Forms and Geometry of Arithmetic Varieties, (1989), 65–87.CrossRefGoogle Scholar
[W] Weil, A., Sur certain groupes d’opérateurs unitaires, Acta Math., 111 (1964), 143–211.Google Scholar