Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T23:47:01.287Z Has data issue: false hasContentIssue false
  • English
  • Français

On proper holomorphic mappings from domains with T-action

Published online by Cambridge University Press:  22 January 2016

Bernard Coupet ,
Yifei Pan  and
Alexandre Sukhov
Bernard Coupet
Affiliation:
LATP, CNRS/UMR n° 6632, CMI, Université de Provence, 39, rue Joliot Curie, 13453 Marseille cedex 13, France
Yifei Pan
Affiliation:
Department of Mathematics, Indiana University-Purdue University Ft. Wayne, Ft. Wayne, IN 46805, U.S.A
Alexandre Sukhov
Affiliation:
LATP, CNRS/UMR n° 6632, CMI, Université de Provence, 39, rue Joliot Curie, 13453 Marseille cedex 13, France
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

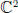We describe the branch locus of a proper holomorphic mapping between two smoothly bounded pseudoconvex domains of finite type in under the assumption that the first domain admits a transversal holomorphic action of the unit circle. As an application we show that any proper holomorphic self-mapping of a smoothly bounded pseudoconvex complete circular domain of finite type in is biholomorphic.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 154 , 1999 , pp. 57 - 72
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1999

References

[1] Alexander, H., Proper holomorphic mappings in ℂn , Indiana Univ. Math. J., 26 (1977), 137–146.CrossRefGoogle Scholar
[2] Baouendi, M., Bell, S. and Rothschild, L.P., Mappings of three-dimensional CR manifolds and their holomorphic extension, Duke Math. J., 56 (1988), 503–530.CrossRefGoogle Scholar
[3] Barrett, D., Regularity of the Bergman projection on domains with transverse symmetries, Math. Ann., 258 (1982), 441–446.CrossRefGoogle Scholar
[4] Barrett, D., Boundary analyticity of proper holomorphic maps of domains with non- analytic boundaries, Math. Ann., 263 (1983), 474–482.CrossRefGoogle Scholar
[5] Bedford, E., Proper holomorphic mappings from strongly pseudoconvex domains, Duke Math. J., 49 (1982), 477–484.CrossRefGoogle Scholar
[6] Bedford, E., Proper holomorphic mappings from domains with real analytic boundary, Amer. J. Math., 106 (1984), 745–760.CrossRefGoogle Scholar
[7] Bedford, E., Action of the automorphisms of a smooth domain in ℂn , Proc. Amer. Math. Soc., 93 (1985), 365–400.Google Scholar
[8] Bedford, E. and Bell, S., Proper self-maps of weakly pseudoconvex domains, Math. Ann., 261 (1982), 505–518.CrossRefGoogle Scholar
[9] Bedford, E. and Fornaess, J.E., A construction of peak functions on weakly pseudo-convex domains, Ann. Math., 270 (1978), 555–568.CrossRefGoogle Scholar
[10] Bell, S., Local boundary behavior of proper holomorphic mappings, Proc. Symp. Pure Math., 41 (1984), 1–7.CrossRefGoogle Scholar
[11] Bell, S. and Catlin, D., Regularity of CR mappings, Math. Z., 199 (1988), 357–368.CrossRefGoogle Scholar
[12] Berteloot, F. and Coeuré, J., Domaines de ℂ2 pseudoconvexes et de type fini ayant un groupe non compact d’automorphismes, Ann. Inst. Fourier, 41 (1991), 77–86.CrossRefGoogle Scholar
[13] Berteloot, F. and Pinchuk, S., Proper holomorphic mappings between bounded complete reinhardt domains in ℂ2 , Math. Z., 219 (1995), 343–356.CrossRefGoogle Scholar
[14] Beteloot, F. and Loeb, J.J., A geometrical characterization of Lattes rational map, Preprint. Univ. d’Angers, 1996.Google Scholar
[15] Carleson, L. and Gamelin, T., Complex dynamics, Springer-Verlag, 1993.CrossRefGoogle Scholar
[16] Catlin, D., Estimates on invariant metrics on pseudoconvex domains of dimension two, Math. Z., 200 (1989), 429–466.CrossRefGoogle Scholar
[17] Coupet, B., Pinchuk, S. and Sukhov, A., On boundary rigidity and regularity of holomorphic mappings, Internat. J. Math., 7 (1996), 617–643.CrossRefGoogle Scholar
[18] Coupet, B. and Sukhov, A., On CR mappings between pseudoconvex hypersurfaces of finite type in ℂ2 , Duke Math. J., 88 (1997), 281–304.CrossRefGoogle Scholar
[19] Diederich, K. and Fornaess, J.E., Pseudoconvex domains: Bounded strictly plurisub-harmonic exhaustion functions, Invent. math., 39 (1977), 371–384.CrossRefGoogle Scholar
[20] Fornaess, J.E. and Sibony, N., Construction of P.S.H. functions on weakly pseudocon-vex domains, Duke Math. J., 58 (1989), 633–656.CrossRefGoogle Scholar
[21] Fornaess, J.E. and Sibony, N., Complex dynamics in higher dimension I, Asterisque, 221 (1994), 201–231.Google Scholar
[22] Huang, X. and Pan, Y., Proper holomorphic mappings between real analytic domains in ℂn , Duke Math. J., 82 (1996), 437–446.CrossRefGoogle Scholar
[23] Hubbard, J. and Papadopol, P., Superattractive fixed points in ℂn , Indiana Univ. Math. J., 43 (1994), 321–365.CrossRefGoogle Scholar
[24] Mumford, D., Alebraic geometry I. Complex projective varieties, Springer Verlag, 1976.Google Scholar
[25] Pan, Y., Proper holomorphic self-mappings of Reinhardt domains, Math. Z., 208 (1991), 289–295.CrossRefGoogle Scholar
[26] Pinchuk, S., Holomorphic inequivalence of some classes of domains in ℂn , Math. USSR Sb., 39 (1981), 61–86.CrossRefGoogle Scholar
[27] Tanaka, N., On the pseudoconformal geometry of hypersurfaces of the space of n complex variables, J. Math. Soc. Japan, 14 (1962), 397–429.CrossRefGoogle Scholar