Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-24T00:39:22.568Z Has data issue: false hasContentIssue false
  • English
  • Français

On positive vector superfunctions of elliptic systems

Published online by Cambridge University Press:  22 January 2016

Kazuya Hayasida  and
Yoshiaki Ikeda
Kazuya Hayasida
Affiliation:
Department of Mathematics, Faculty of Science, Kanazawa University, Kanazawa, 920Japan
Yoshiaki Ikeda
Affiliation:
Department of Mathematics, Aichi University of Education, Kariya, 448, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Ω be a bounded domain in Rn with coordinates x = (x1, …, xn) such that Ω contains the origin. We consider the elliptic operators

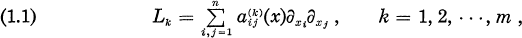
where 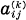are real valued and in C2(Ω).

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 92 , December 1983 , pp. 51 - 67
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1983

References

[1] Akô, K., Semi-decomposable systems and vector subfunctions, Funkcial. Ekvac, 8 (1966), 91–97.Google Scholar
[2] Ancona, A., Une propriété d’invariance des ensembles absorbants par perturbation d’un opérateur elliptique, Comm. Partial Differential Equations, 4 (1979), 321–337.CrossRefGoogle Scholar
[3] Hayasida, K., Tachi, H., On the three circles theorem for solutions of elliptic equations, to appear in Funkcial. Ekvac.Google Scholar
[4] Hildebrandt, S., Widman, K. O., Variational inequalities for vector-valued functions, J. Reine Angew. Math., 309 (1979), 191–220.Google Scholar
[5] John, F., Continuous dependence on data for solutions of partial differential equations with a prescribed bound, Comm. Pure Appl. Math., 8 (1960), 551–585.CrossRefGoogle Scholar
[6] Kondrat’ev, V. A., Èidel’man, S. D., Positive solutions of linear partial differential equations, Trans. Moscow Math. Soc., 31 (1974), 81–148.Google Scholar
[7] Mandras, F., Disegualianza di Harnack per sistemi ellitici debolmente accoppiati, Boll. Un. Mat. Ital., A (5), 14 (1977), 313–321.Google Scholar