Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-01-11T13:10:47.084Z Has data issue: false hasContentIssue false
  • English
  • Français

On polylogarithms*)

Published online by Cambridge University Press:  22 January 2016

Johan L. Dupont
Johan L. Dupont*
Affiliation:
Matematisk Institut, Aarhus Universitet, Ny Munkegade, DK-8000 Aarhus C, Denmark
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Some functions related to the complex dilogarithmic function

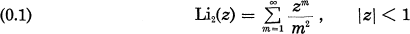
(in the notation of Lewin [9]) are known to occur in connection with algebraic K-theory and characteristic classes (see e.g. Bloch [1], Gelfand-MacPherson [7], Dupont [5], and the references given there). Recently MacPherson and Hain (see [10]) has announced results of a similar kind for some higher polylogarithmic functions. Also Ramakrishnan [11] and [12] has recently studied the classical polylogarithms, which for |z| < 1 are given by

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 114 , June 1989 , pp. 1 - 20
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1989

Footnotes

*)

This work is partially supported by grants from Statens Naturvidenskabelige Forskningsråd, Denmark, and the National Science Foundation, U.S.A.

References

[1] Bloch, S., Applications of the dilogarithm function in algebraic geometry, in: Nagata, M., ed., International Symposium on Algebraic Geometry, Kyoto, 1977, pp. 103–114, Kinokuniya Book-Store Co., Tokyo, 1978.Google Scholar
[2] Bloch, S., Higher regulators, algebraic K-theory and zeta functions of elliptic curves, Lectures given at the University of California at Irvine, Preprint, 1978.Google Scholar
[3] Chen, K.-T., Iterated path integrals, Bull. Amer. Math. Soc, 83 (1977), 831–879.Google Scholar
[4] Deligne, P., Equations Différentielles à Points Singuliers Réguliers, Lecture Notes in Mathematics, 163, Springer-Verlag, Berlin-Heidelberg-New York, 1970.Google Scholar
[5] Dupont, J. L., The dilogarithm as a characteristic class for flat bundles, J. Pure Appl. Algebra, 44 (1987), 137–164.Google Scholar
[6] Dupont, J. L. and Sah, C.-H., in preparation.Google Scholar
[7] Gelfand, I. M. and MacPherson, R. D., Geometry in Grassmannians and a generalization of the dilogarithm, Adv. in Math., 44 (1982), 279–312.Google Scholar
[8] Hain, R. M., The geometry of the mixed Hodge structure on the fundamental group, preprint, University of Washington, Seattle.Google Scholar
[9] Lewin, L., Polylogarithms and Associated Functions, North Holland, New York-Oxford, 1981.Google Scholar
[10] MacPherson, R. D., Grassmannian cohomology, preprint.Google Scholar
[11] Ramakrishnan, D., On the monodromy of higher logarithms, Proc. Amer. Math. Soc, 85 (1982), 596–599.Google Scholar
[12] Ramakrishnan, D., Analogs of the Bloch-Wigner function for higher polylogarithms, in: Bloch, S., Dennis, R. K., Friedlander, E. M., Stein, M. R., eds., Applications of Algebraic K-theory to Algebraic Geometry and Number Theory, Contemporary Mathematics Vol. 55, Part I, pp. 371–376, Amer. Math. Soc, Providence R. I., 1986.CrossRefGoogle Scholar
[13] Ree, R., Lie elements and an algebra associated with shuffles, Ann. of Math., 68 (1958), 210–220.Google Scholar
[14] Sah, C.-H., Homology of classical Lie groups made discrete, III, J. Pure Appl. Algebra, 56 (1989), 269–312.Google Scholar