Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Greenberg, Ralph
1977.
Onp-adicL-functions and cyclotomic fields. II.
Nagoya Mathematical Journal,
Vol. 67,
Issue. ,
p.
139.
Ferrero, Bruce
and
Greenberg, Ralph
1978.
On the behavior ofp-adicL-efunctions ats=0.
Inventiones Mathematicae,
Vol. 50,
Issue. 1,
p.
91.
Greenberg, Ralph
1978.
On 2-adicL-functions and cyclotomic invariants.
Mathematische Zeitschrift,
Vol. 159,
Issue. 1,
p.
37.
Schneider, Peter
1979.
�ber gewisse Galoiscohomologiegruppen.
Mathematische Zeitschrift,
Vol. 168,
Issue. 2,
p.
181.
Wiles, Andrew
1980.
Modular curves and the class group of Q(? p ).
Inventiones Mathematicae,
Vol. 58,
Issue. 1,
p.
1.
Greenberg, Ralph
1982.
Number Theory Related to Fermat’s Last Theorem.
Vol. 26,
Issue. ,
p.
275.
Greenberg, Ralph
1983.
Onp-adic ArtinL-functions.
Nagoya Mathematical Journal,
Vol. 89,
Issue. ,
p.
77.
Mazur, B.
and
Wiles, A.
1984.
Class fields of abelian extensions of Q.
Inventiones Mathematicae,
Vol. 76,
Issue. 2,
p.
179.
Kuz'min, L. V.
1987.
Algebraic number fields.
Journal of Soviet Mathematics,
Vol. 38,
Issue. 3,
p.
1930.
Rognes, J.
Weibel, C.
and
M. Kolster, appendix by
1999.
Two-primary algebraic 𝐾-theory of rings of integers in number fields.
Journal of the American Mathematical Society,
Vol. 13,
Issue. 1,
p.
1.
Aoki, Miho
2001.
The Iwasawa Main Conjecture and Gauss Sums.
Journal of Number Theory,
Vol. 89,
Issue. 1,
p.
151.
Skinner, Christopher
and
Urban, Eric
2014.
The Iwasawa Main Conjectures for GL2.
Inventiones mathematicae,
Vol. 195,
Issue. 1,
p.
1.
ICHIMURA, HUMIO
NAKAJIMA, SHOICHI
and
SUMIDA-TAKAHASHI, HIROKI
2014.
ON THE 2-ADIC IWASAWA LAMBDA INVARIANTS OF THE p-CYCLOTOMIC FIELDS AND THEIR QUADRATIC TWISTS.
International Journal of Number Theory,
Vol. 10,
Issue. 02,
p.
283.
Blumberg, Andrew
and
Mandell, Michael
2017.
The nilpotence theorem for the algebraic
K–theory of the sphere spectrum.
Geometry & Topology,
Vol. 21,
Issue. 6,
p.
3453.


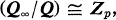 the additive group of
the additive group of 