Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T23:58:30.021Z Has data issue: false hasContentIssue false
  • English
  • Français

On p-adic L-functions and cyclotomic fields. II

Published online by Cambridge University Press:  22 January 2016

Ralph Greenberg
Ralph Greenberg*
Affiliation:
Brandeis University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

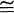Let p be a prime. If one adjoins to Q all pn-th roots of unity for n = 1,2,3, …, then the resulting field will contain a unique subfield Q∞ such that Q∞ is a Galois extension of Q with Gal (Q∞/Q) Zp, the additive group of p-adic integers. We will denote Gal (Q∞/Q) by Γ. In a previous paper [6], we discussed a conjecture relating p-adic L-functions to certain arithmetically defined representation spaces for Γ. Now by using some results of Iwasawa, one can reformulate that conjecture in terms of certain other representation spaces for Γ. This new conjecture, which we believe may be more susceptible to generalization, will be stated below.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 67 , August 1977 , pp. 139 - 158
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1977

References

[1] Brumer, A., On the units of algebraic number fields, Mathematika, 14 (1967), 121–124.Google Scholar
[2] Coates, J., p-adic L-functions and Iwasawa theory, to appear in Proceedings of symposium on algebraic number theory held in Durham, England, 1975.Google Scholar
[3] Coates, J., Lichtenbaum, S., On l-adic zeta functions, Ann. of Math., 98 (1973), 498–550.Google Scholar
[4] Ferrero, B., Iwasawa invariants of abelian number fields, to appear.Google Scholar
[5] Gras, G., Classes d’ideaux des corps abeliens et nombres de Bernoulli generalises, Ann. Inst. Fourier, 27 (1977), 1–66.Google Scholar
[6] Greenberg, R., On p-adic L-functions and cyclotomic fields, Nagoya Math. Jour., 56 (1975), 61–77.CrossRefGoogle Scholar
[7] Greenberg, R., On the Iwasawa invariants of totally real number fields, Amer. Jour, of Math., 98 (1976), 263–284.Google Scholar
[8] Hasse, H., Uber die Klassenzahl abelscher Zahlkorper, Akademie Verlag, Berlin, 1952.Google Scholar
[9] Iwasawa, K., Lectures on p-adic L-functions, Ann. Math. Studies 74, Princeton University Press, 1972.Google Scholar
[10] Iwasawa, K., On Zl -extensions of algebraic number fields, Ann. of Math., 98 (1973), 246–326.Google Scholar
[11] Kubota, T., Leopoldt, H., Eine p-adische Theorie der Zetawerte (Teil I), J. Reine Angew. Math., 213 (1964), 328–339.Google Scholar
[12] Leopoldt, H., Uber Einheitengruppe und Klassenzahl reeller abelscher Zahlkorper, Abh. Deutsche Akad. Wiss. Berlin Math. 2. (1954).Google Scholar