Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T23:35:51.701Z Has data issue: false hasContentIssue false
  • English
  • Français

On non-elliptic boundary problems

Published online by Cambridge University Press:  22 January 2016

Yoshio Kato
Yoshio Kato*
Affiliation:
Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The purpose of this paper is to study the boundary value problems for the second order elliptic differential equation

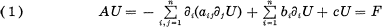
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 86 , June 1982 , pp. 1 - 38
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1982

References

[ 1 ] Egorov, Ju. V. and Kondrat’ev, V. A., The oblique derivative problems, Mat. Sbornik, 78 (1969), 148–176. = Math. USSR Sbornik, 7 (1969), 139–169.Google Scholar
[ 2 ] örmander, L. H, Pseudo-differential operators and non-elliptic boundary problem Ann. of Math., 83 (1966), 129–209.Google Scholar
[ 3 ] Kato, Y., Mixed-type boundary condition for second order elliptic differential equations, J. Math. Soc. Japan, 26 (1974), 405–432.Google Scholar
[ 4 ] Kato, Y., On a class of non-elliptic boundary problems, Nagoya Math. J., 54 (1974), 7–20.Google Scholar
[ 5 ] Kato, Y., Another approach to a non-elliptic boundary problem, Nagoya Math. J., 66 (1977), 13–22.Google Scholar
[ 6 ] Maljutov, M. B., On the Poincaré boundary value problem, Trans. Moscow Math. Soc, 20 (1969), 173–204.Google Scholar
[ 7 ] Soga, H., Boundary value problems with oblique derivative Publ. RIMS, Kyoto Univ., 10 (1975), 619–668.CrossRefGoogle Scholar
[ 8 ] Winzell, B., Solutions of second order elliptic partial differential equations with prescribed directional derivative on the boundary, Dissertation.Google Scholar
[ 9 ] Yosida, K., Functional analysis, Springer-Verlag (1965).Google Scholar