Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-01-11T10:03:56.603Z Has data issue: false hasContentIssue false
  • English
  • Français

On nilpotent factors of congruent ideal class groups of Galois extensions

Published online by Cambridge University Press:  22 January 2016

Yoshiomi Furuta
Yoshiomi Furuta*
Affiliation:
Kanazawa University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let K be a Galois extension of an algebraic number field k of finite degree with Galois group g. Then g acts on a congruent ideal class group 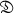of K as a group of automorphisms, when the class field M over K corresponding to 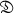is normal over K. Let Ig be the augmentation ideal of the group ring Zg over the ring of integers Z, namely Ig be the ideal of Zg generated by σ − 1, σ running over all elements of g. Then 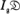is the group of all elements aσ-1 where a and σ belong to 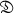and g respectively.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 62 , September 1976 , pp. 13 - 28
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1976

References

[1] Babakhanian, A., Cohomological methods in group theory, Marcel Dekker, Inc., New York (1972).Google Scholar
[2] Barrucand, P. and Cohn, H., Note on primes of type x 2 + 32y2 , class number, and residuacity, J. Reine Angew, Math., 238 (1969), 67–70.Google Scholar
[3] Fröhlich, A., The genus field and genus group in finite number fields I, II, Mathematika, 6 (1959), 40–46, 142–146.Google Scholar
[4] Furuta, Y., The genus field and genus number in algebraic number fields, Nagoya Math. J., 29 (1967), 281–285.Google Scholar
[5] Furuta, Y., Über die zentrale Klassenzahl eines relativ-galoisschen Zahlkörpers, J. Number Theory, 3 (1971), 318–322.Google Scholar
[6] Furuta, Y., On class field towers and the rank of ideal class groups, Nagoya Math. J., 48 (1972), 147–157.Google Scholar
[7] Gras, G., Sur le D-groupe des classes des extensions cycliques de degré premier D , C. R. Acad. Sci. Paris, 274 (1972), 1145–1148.Google Scholar
[8] Gras, G., Sur le D-classes d’ideaux dans les extensions cycliques relatives de degré premier D , Ann. Inst. Fourier, Grenoble, 23, 3 (1973), 1–48; 23, 4 (1973), 1–44.Google Scholar
[9] Hasse, H., Über die Klassenzahl des Körpers P mit einer Primzahl p = 1 mod. 23 , Aequations Mathematicae, 3 (1969), 165–169.Google Scholar
[10] Hasse, H., Über die Teilbarkeit durch 23 der Klassenzahl der quadratischen Zahlkörper mit genau zwei verschiedenen Diskriminantenprimteilern, Math. Nachr., 46 (1970), 61–70.Google Scholar
[11] Masuda, K., An application of the generalized norm residue symbol, Proc. Amer. Math. Soc., 10 (1959), 245–252.Google Scholar