Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ito, Noboru
1962.
On Transitive Simple Groups of Degree 3p.
Nagoya Mathematical Journal,
Vol. 21,
Issue. ,
p.
123.
Ito, Noboru
1963.
Transitive permutation groups of degree 𝑝=2𝑞+1,𝑝 and 𝑞 being prime numbers.
Bulletin of the American Mathematical Society,
Vol. 69,
Issue. 2,
p.
165.
Iţo, Noboru
1964.
Transitive permutation groups of degree 𝑝=2𝑞+1, 𝑝 and 𝑞 being prime numbers. II.
Transactions of the American Mathematical Society,
Vol. 113,
Issue. 3,
p.
454.
Foulkes, H.O.
1970.
Group transitivity and a multiplicative function of a partition.
Journal of Combinatorial Theory,
Vol. 9,
Issue. 3,
p.
261.
Zalcstein, Yechezkel
1971.
Studies in the representation theory of finite semigroups.
Transactions of the American Mathematical Society,
Vol. 161,
Issue. 0,
p.
71.
Saxl, Jan
1975.
Characters of multiply transitive permutation groups.
Journal of Algebra,
Vol. 34,
Issue. 3,
p.
528.
Klemm, Michael
1976.
�ber Charaktere mehrfach transitiver Gruppen.
Archiv der Mathematik,
Vol. 27,
Issue. 1,
p.
241.
Saxl, Jan
1977.
Combinatoire et Représentation du Groupe Symétrique.
Vol. 579,
Issue. ,
p.
258.
Kerber, Adalbert
1978.
A matrix of combinatorial numbers related to the symmetric groups.
Discrete Mathematics,
Vol. 21,
Issue. 3,
p.
319.
Klemm, Michael
and
Wagner, Bernd
1979.
A matrix of combinatorial numbers related to the symmetric groups.
Discrete Mathematics,
Vol. 28,
Issue. 2,
p.
173.
Merris, Russell
and
Watkins, William
1983.
Tensors and Graphs.
SIAM Journal on Algebraic Discrete Methods,
Vol. 4,
Issue. 4,
p.
534.
Cameron, P.J
Deza, M
and
Frankl, P
1987.
Sharp sets of permutations.
Journal of Algebra,
Vol. 111,
Issue. 1,
p.
220.
Bernstein, M.
and
Sloane, N.J.A.
1995.
Some canonical sequences of integers.
Linear Algebra and its Applications,
Vol. 226-228,
Issue. ,
p.
57.
Aldhafeeri, S.
Curtis, R. T.
and
Werner, Frank
2011.
A Character Condition for Quadruple Transitivity.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2011,
Issue. 1,
Rahmani, Mourad
2013.
The Akiyama–Tanigawa matrix and related combinatorial identities.
Linear Algebra and its Applications,
Vol. 438,
Issue. 1,
p.
219.
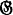 has an irreducible character χ1 such that χ1(R) = α(R) − 1 for any element R of
has an irreducible character χ1 such that χ1(R) = α(R) − 1 for any element R of 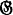 and a quadruply transitive group has irreducible characters χ3 and χ3 such that χ2(R) =
and a quadruply transitive group has irreducible characters χ3 and χ3 such that χ2(R) = 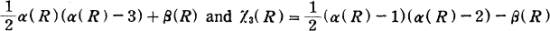 where α(R) and β(R) are respectively the numbers of one cycles and two cycles contained in R. G. Frobenius was led to this fact in the connection with characters of the symmetric groups and he proved the following interesting theorem: if a permutation group
where α(R) and β(R) are respectively the numbers of one cycles and two cycles contained in R. G. Frobenius was led to this fact in the connection with characters of the symmetric groups and he proved the following interesting theorem: if a permutation group 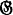 of degree n is t-ply transitive, then any irreducible character of the symmetric group of degree n with dimension at most equal to
of degree n is t-ply transitive, then any irreducible character of the symmetric group of degree n with dimension at most equal to 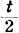 is an irreducible character of
is an irreducible character of 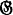 .
.