Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Matsumoto, Kikuji
1968.
Positively Infinite Singularities of a Superharmonic Function.
Nagoya Mathematical Journal,
Vol. 31,
Issue. ,
p.
89.


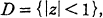 , with circumference
, with circumference 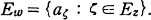 It is known that
It is known that 