Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T23:42:04.937Z Has data issue: false hasContentIssue false
  • English
  • Français

On Meromorphic Mappings into Taut Complex Analytic Spaces

Published online by Cambridge University Press:  22 January 2016

Toshio Urata
Toshio Urata*
Affiliation:
Aichi University of Education
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we study a certain difference between meromorphic mappings and holomorphic mappings into taut complex analytic spaces. We prove in §2 that, for any complex analytic space X, there exists a unique proper modification 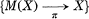of X with center Sg (X) which is minimal with respect to the property that M(X) is normal and, for any T-meromorphic mapping f: X → Y (see Definition 1.3) into a complex analytic space Y, there exists a unique holomorphic mapping 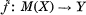such that 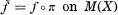except some nowhere dense complex analytic set, where Sg(X) denotes the set of all singular points of X.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 50 , June 1973 , pp. 49 - 65
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1973

References

[1] Barth, T. J.: Taut and tight complex manifolds, Proc. Amer. Math. Soc, 24 (1970), 429–431.Google Scholar
[2] Cartan, H.: Quotients of complex analytic spaces, In Contributions of Function Theory, Tata Institute, Bombay, (1960), 1–15.Google Scholar
[3] Fujimoto, H.: On holomorphic mappings into a taut complex space, Nagoya Math. J., 46 (1971), 49–61.Google Scholar
[4] Grauert, H. und Kerner, H.: Deformationen von Singularitaten komplexer Raume, Math. Ann., 153 (1964), 236–260.Google Scholar
[5] Hironaka, H.: Resolution of singularities of an algebraic variety over a field of characteristic zero, Ann. of Math., 79 (1964), 109–326.Google Scholar
[6] Holman, H.: Local properties of holomorphic mappings, Proc. Conf. on Complex Analysis, Mineapolis (1964), 94–109.Google Scholar
[7] Kaup, W.: Hyperbolische komplexe Raume, Ann. Inst. Fourier (Grenoble), 18 (1968), 303–330.Google Scholar
[8] Kaup, W.: Reele Transformationsgruppe und invariante Metriken auf komplexen Raumen, Inventiones math., 3 (1970), 43–70.Google Scholar
[9] Kiernan, P. J.: On the relation between taut, tight and hyperbolic manifolds, Bull. Am. Math. Soc, 76 (1967), 49–51.CrossRefGoogle Scholar
[10] Kobayashi, S.: Invariant distances on complex manifolds and holomorphic mappings, J. Math. Soc. Japan, 19 (1967), 460–480.Google Scholar
[11] Kobayashi, S.: Hperbolic manifolds and holomorphic mappings, Marcel Dekker, Inc., New York, 1970.Google Scholar
[12] Kwack, M. H.: Generalization of the big Picard theorem, Ann. Math., 90 (1969), 13–22.CrossRefGoogle Scholar
[13] Wagreich, P.: Elliptic singularities of surfaces, Amer. J. Math., 92 (1970), 419–454.CrossRefGoogle Scholar
[14] Wu, H.: Normal family of holomorphic mappings, Acta Math., 119 (1967), 194–329.CrossRefGoogle Scholar