Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-22T11:40:21.237Z Has data issue: false hasContentIssue false
  • English
  • Français

On Herstein’s Theorem Concerning Three Fields

Published online by Cambridge University Press:  22 January 2016

Carl Faith
Carl Faith*
Affiliation:
Institute for Advanced Study, Princeton, N. J.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let L > K ≧ Φ, L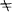K, be three fields such that: (1) L/K is not purely inseparable, and (2) L/Φ is transcendental. Then Herstein’s theorem [2] asserts the existence of u ∈ L such that f(u) ∉ K for every non-constant polynomial f(X) ∈ Φ[X].

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 19 , October 1961 , pp. 49 - 53
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1961

References

[1] Faith, Carl, A structure theory for semialgebraic extensions of division algebras, Journal für die reine und angewandte Mathematik, (1961).Google Scholar
[2] Herstein, I. N., A theorem concerning three fields, Canadian Journal of Mathematics, vol. 7 (1955), 202–203.Google Scholar
[3] Waerden, B. L. van der, Algebra I, Vierte Auflage, Berlin-Göttingen-Heidelberg, 1955.Google Scholar
[4] Zariski, O., Interprétation algébrico-géométriques du quatorzième problème de Hilbert, Bull. Sci. Math. vol. 78 (1954), 155–168.Google Scholar