Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Nomura, Yasutoshi
1967.
Remark on the Dual EHP Sequence.
Nagoya Mathematical Journal,
Vol. 29,
Issue. ,
p.
269.
Nomura, Yasutoshi
1972.
Iterated loop spaces.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 48,
Issue. 9,
Mather, Michael
and
Walker, Marshall
1980.
Commuting homotopy limits and colimits.
Mathematische Zeitschrift,
Vol. 175,
Issue. 1,
p.
77.
Alonso, Juan M.
1983.
Fibrations that are cofibrations.
Proceedings of the American Mathematical Society,
Vol. 87,
Issue. 4,
p.
749.
Kahn, Peter J.
1984.
Some function spaces of CW type.
Proceedings of the American Mathematical Society,
Vol. 90,
Issue. 4,
p.
599.
Dula, Giora
and
Marcum, Howard J.
1995.
Hopf invariants of the Berstein-Hilton-Ganea kind.
Topology and its Applications,
Vol. 65,
Issue. 2,
p.
179.
Marcum, Howard J.
1996.
FUNCTORIAL PROPERTIES OF THE HOPF INVARIANT I.
Quaestiones Mathematicae,
Vol. 19,
Issue. 3-4,
p.
537.
Blanc, David
2008.
Comparing homotopy categories.
Journal of K-Theory,
Vol. 2,
Issue. 1,
p.
169.
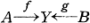 (cf. [13]) is determined by those of f and g (see Theorem 3.4).
(cf. [13]) is determined by those of f and g (see Theorem 3.4).