Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Binia, J.
Zakai, M.
and
Ziv, J.
1974.
On the<tex>epsilon</tex>-entropy and the rate-distortion function of certain non-Gaussian processes.
IEEE Transactions on Information Theory,
Vol. 20,
Issue. 4,
p.
517.
Binia, J.
1974.
On the<tex>epsilon</tex>-entropy of certain Gaussian processes.
IEEE Transactions on Information Theory,
Vol. 20,
Issue. 2,
p.
190.
Luschgy, Harald
and
Pagès, Gilles
2004.
Sharp asymptotics of the functional quantization problem for Gaussian processes.
The Annals of Probability,
Vol. 32,
Issue. 2,
Luschgy, Harald
and
Pagès, Gilles
2014.
Constructive quadratic functional quantization and critical dimension.
Electronic Journal of Probability,
Vol. 19,
Issue. none,


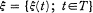 be a stochastic process, where
be a stochastic process, where 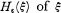 is defined as the following quantity:
is defined as the following quantity: