Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shibata, Y.
1981.
Singularities in Boundary Value Problems.
p.
213.
Jäger, Willi
and
Rejto, Peter
1983.
Limiting absorption principle for some Schrödinger operators with exploding potentials, II.
Journal of Mathematical Analysis and Applications,
Vol. 95,
Issue. 1,
p.
169.
2017.
Spectral and Scattering Theory for Second-Order Partial Differential Operators.
p.
219.
Mochizuki, Kiyoshi
2020.
Advances in Harmonic Analysis and Partial Differential Equations.
p.
209.


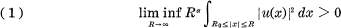
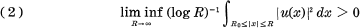
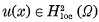 of the equation
of the equation