Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T14:31:53.248Z Has data issue: false hasContentIssue false
  • English
  • Français

On Doubly Transitive Groups of Degree n and Order 2(n − 1)n

Published online by Cambridge University Press:  22 January 2016

Noboru Ito
Noboru Ito*
Affiliation:
Mathematical Institute, Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

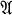Let 5 denote the icosahedral group and let 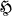be the normalizer of a Sylow 5-subgroup of 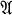5. Then the index of 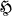in 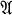5 equals six. Let us represent 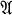5 as a permutation group A on the set of residue classes of 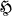with respect to 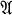5 Then it is clear that A is doubly transitive of degree 6 and order 60 = 2·5·6. Since 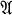5 is simple, A does not contain a regular normal subgroup.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 27 , Issue 2 , July 1966 , pp. 409 - 417
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1966

References

[1] Brauer, R., On the representations of groups of finite order, Proc. Nat. Acad. Sci. U.S.A. 25, 290–295 (1939).Google Scholar
[2] Holyoke, T., Transitive extens ons of dihedral groups, Math. Zeitschr. 60, 79–80 (1954).Google Scholar
[3] Ito, N., Remarks on factorizable groups. Acta Sci. Math. Szeged 15, 83–84 (1951).Google Scholar
[4] Wielandt, H., Finite permutation groups, Academic Press, New York-London (1964).Google Scholar
[5] Zassenhaus, H., Lehrbuch der Gruppentheorie, I, Teubner, Leipzig (1937).Google Scholar