Article contents
On Crossed Products of a Sfield
Published online by Cambridge University Press: 22 January 2016
Extract
In the previous paper [3] the author has shown a possibility to construct a series of sfields by taking sfields of quotients of split crossed products of a sfield. In this paper the same problem is treated, and, by considering general crossed products, a generalization of the previous result is given: Let K be a sfield and G be the join of a well-ordered ascending chain of groups Gα of outer automorphisms of K such that a) G1 is the identity automorphism group, b) Gα is a group extension of Gα-1 by a torsion-free abelian group for each non-limit ordinal α, and c) 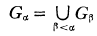 for each limit ordinal α. Then an arbitrary crossed product of K with G is an integral domain with a sfield of quotients Q and the commutor ring of K in Q coincides with the centre of K.
for each limit ordinal α. Then an arbitrary crossed product of K with G is an integral domain with a sfield of quotients Q and the commutor ring of K in Q coincides with the centre of K.
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1963
References
- 3
- Cited by


