Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gotô, Morikuni
and
Yamabe, Hidehiko
1951.
On Some Properties of Locally Compact Groups with no Small Subgroup.
Nagoya Mathematical Journal,
Vol. 2,
Issue. ,
p.
29.
Kuranishi, Masatake
1952.
On One-parameter Subgroups in Finite Dimensional Locally Compact Group with No Small Subgroups.
Nagoya Mathematical Journal,
Vol. 4,
Issue. ,
p.
89.
Hano, Jun-Ichi
and
Morimoto, Akihiko
1955.
Note on the Group of Affine Transformations of an Affinely Connected Manifold.
Nagoya Mathematical Journal,
Vol. 8,
Issue. ,
p.
71.
Chu, Hsin
and
Kobayashi, Shoshichi
1964.
The automorphism group of a geometric structure.
Transactions of the American Mathematical Society,
Vol. 113,
Issue. 1,
p.
141.
Fujimoto, Hirotaka
1968.
On The Holomorphic Automorphism Groups of Complex Spaces.
Nagoya Mathematical Journal,
Vol. 33,
Issue. ,
p.
85.
Kellum, Mark
1993.
Uniformly quasi-isometric foliations.
Ergodic Theory and Dynamical Systems,
Vol. 13,
Issue. 1,
p.
101.
Isaev, A. V.
2015.
Proper actions of high-dimensional groups on complex manifolds.
Bulletin of Mathematical Sciences,
Vol. 5,
Issue. 2,
p.
251.
Khan, Qayum
2018.
Countable approximation of topological G-manifolds: Compact Lie groups G.
Topology and its Applications,
Vol. 235,
Issue. ,
p.
14.


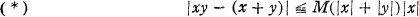
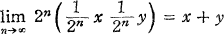 .
.