Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ribet, Kenneth A.
1977.
Modular Functions of one Variable V.
Vol. 601,
Issue. ,
p.
18.
Ligozat, Gérard
1979.
Courbes elliptiques ayant bonne réduction en dehors de 3.
Nagoya Mathematical Journal,
Vol. 76,
Issue. ,
p.
115.
Ribet, Kenneth A.
1980.
Twists of modular forms and endomorphisms of Abelian varieties.
Mathematische Annalen,
Vol. 253,
Issue. 1,
p.
43.
Momose, Fumiyuki
1983.
Galois action on some ideal section points of the abelian variety associated with a modular form and its application.
Nagoya Mathematical Journal,
Vol. 91,
Issue. ,
p.
19.
Hasegawa, Yuji
1996.
On some examples of modular QM-abelian surfaces.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 72,
Issue. 1,


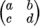 with
with 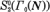 be the “essential part” of
be the “essential part” of 