Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Goto, Shiro
1982.
Buchsbaum rings of maximal embedding dimension.
Journal of Algebra,
Vol. 76,
Issue. 2,
p.
383.
Goto, Shiro
1982.
Buchsbaum rings with multiplicity 2.
Journal of Algebra,
Vol. 74,
Issue. 2,
p.
494.
Goto, Shiro
1983.
On the associated graded rings of parameter ideals in Buchsbaum rings.
Journal of Algebra,
Vol. 85,
Issue. 2,
p.
490.
Goto, Shiro
1984.
Noetherian local rings with Buchsbaum associated graded rings.
Journal of Algebra,
Vol. 86,
Issue. 2,
p.
336.
Goto, Shiro
and
Suzuki, Naoyoshi
1984.
Index of reducibility of parameter ideals in a local ring.
Journal of Algebra,
Vol. 87,
Issue. 1,
p.
53.
Brodmann, Markus
and
Schenzel, Peter
2006.
Arithmetic properties of projective varieties of almost minimal degree.
Journal of Algebraic Geometry,
Vol. 16,
Issue. 2,
p.
347.
Endo, Naoki
Goto, Shiro
Iai, Shin-ichiro
and
Matsuoka, Naoyuki
2023.
When are the rings I:I Gorenstein?.
Communications in Algebra,
Vol. 51,
Issue. 4,
p.
1721.
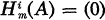 for i ≠ 1, dim A.
for i ≠ 1, dim A.