Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T23:27:53.012Z Has data issue: false hasContentIssue false
  • English
  • Français

On Boundary Value Problems for Elliptic Equations in a Singular Domain

Published online by Cambridge University Press:  22 January 2016

Kazunari Hayashida
Kazunari Hayashida*
Affiliation:
Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. Let Ω be a bounded domain in the plane and denotes its closure and boundary by Ω̅ and ∂Ω, respectively. We shall say that the domain Ω is regular, if every point P ∈ ∂û has an 2-dimensional neighborhood U such that dΩ ∩ U can be mapped in a one-to-one way onto a portion of the tangent line through P by a mapping T which together with its inverse is infinitely differentiable. Let L be an elliptic operator of order 2m defined in Ω̅ and let 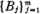be a normal set of boundary operators of orders mf <2m. If f is a given function in Ω, the boundary value problem II(L,f,Bj) will be to find a solution u of

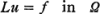
satisfying

Bju = 0 on ∂Ω, j = 1, …, m.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 36 , November 1969 , pp. 99 - 115
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1969

References

[1] Agmon, S., Douglis, A., and Nirenberg, L., Estimates near the boundary for solutions of elliptic partial differential equations satisfying general boundary conditions I, Comm. Pure Appl. Math., 12, 1959, pp. 623–727.Google Scholar
[2] Agmon, S., Douglis, A., and Nirenberg, L., II, ibid. 17, 1964, pp. 35–92.Google Scholar
[3] Aronszajn, N., and Milgram, A.N., Differential operators on Riemannian manifolds, Rend. Circ. Mat. Parlermo, Ser. 2, 2, pp. 1–61.Google Scholar
[4] Ikebe, N., On elliptic boundary value problems with discontinuous coefficients, Memoirs of the Fac. Sci. Kyushu Univ., Ser. A, 21, 1967, pp. 167–184.Google Scholar
[5] Koppelman, W., and Pincus, J.V., Spectral representations of finite Hilbert transformations, Math. Z., 71, 1959, pp. 399–407.Google Scholar
[6] Lax, P. D., and Milgram, A., Parabolic equations, Contributions to the Theory of Partial Differential Equations, Ann. of Math. Studies, Princeton University Press, 1954, pp. 167–190.Google Scholar
[7] Peetre, J., Mixed problems for higher order elliptic equations in two variables (I), Annali di Pisa, 15, 1961, pp. 337–353.Google Scholar
[8] Schechter, M., General boundary value problems for elliptic partial differential equations, Comm. Pure Appl. Math., 12, 1959, pp. 451–485.Google Scholar
[9] Schechter, M., Mixed boundary problems for general elliptic equations, Comm. Pure Appl. Math., 13, 1960, pp. 407–425.Google Scholar
[10] Schechter, M., A generalization of the problem of transmission, Annali della Scoula Norm. Sup. Pisa., Ser. 3, 13, 1960, pp. 207–236.Google Scholar
[11] Shamir, E., Reduced Hilbert transforms and singular integral equations, J. D’analyse Math., 12, 1964, pp. 277–305.Google Scholar
[12] Shamir, E., Mixed boundary value problems for elliptic equations in the plane. The Lp theory, Annali di Pisa, 17, 1963, pp. 117–139.Google Scholar
[13] Shamir, E., Elliptic systems of singular integral operators. I. The half-space case, Trans. Amer. Math. Soc, 124, 1967, pp. 107–124.Google Scholar
[14] Schwartz, J., Some results on the spectra and spectral resolutions of a class of singular integral operators, Comm. Pure Appl. Math., 15, 1962, pp. 75–90.Google Scholar
[15] Widom, H., Singular integral equations in Lp , Trans. Amer. Math. Soc, 97, 1960, pp. 131–159.Google Scholar