Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-05T02:34:33.520Z Has data issue: false hasContentIssue false
  • English
  • Français

On area integrals and radial variations of analytic functions in the unit disk

Published online by Cambridge University Press:  22 January 2016

Takafumi Murai
Takafumi Murai*
Affiliation:
Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We are concerned with the behaviour of analytic functions near the boundary. Let T and D be the unit circle |z| = 1 and the unit disk |z| < 1, respectively. The element of T is denoted by θ (0 ≤ θ < 2π). Let 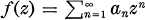be analytic in D. The area integral A(f, θ) of f at θ is defined by

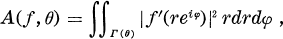
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 61 , July 1976 , pp. 135 - 159
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1976

References

[1] Kahane, J. P.; Some random series of functions, Raytheon education company, 1968.Google Scholar
[2] Lohwater, A. J. and Piranian, G.; On a conjecture of Lusin, Michigan Math. J., (1955), p. 63–68.Google Scholar
[3] Offord, A. C.; Distribution of values of random function in the unit disk, Studia Math., (1972), p. 71–106.CrossRefGoogle Scholar
[4] Zygmund, A.; Trigonometric series II, Cambridge, 1959.Google Scholar