Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
NAGASE, Haruo
1989.
On an asymptotic behaviour of solutions of nonlinear parabolic variational inequalities.
Japanese journal of mathematics. New series,
Vol. 15,
Issue. 1,
p.
169.
Nagase, Haruo
2000.
On a regularity property and a priori estimates for solutions of nonlinear parabolic variational inequalities.
Nagoya Mathematical Journal,
Vol. 160,
Issue. ,
p.
123.


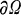 of class
of class 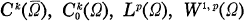 and
and 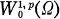 are known.
are known.