Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-10T08:01:21.305Z Has data issue: false hasContentIssue false
  • English
  • Français

On Abstract Wiener Measure*

Published online by Cambridge University Press:  22 January 2016

Balram S. Rajput
Balram S. Rajput*
Affiliation:
Departments of Mathematics and Statistics, University of North Carolina, Chapel Hill, N.C. 27514
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

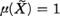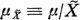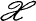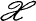In a recent paper, Sato [6] has shown that for every Gaussian measure n on a real separable or reflexive Banach space (X, ‖ • ‖) there exists a separable closed sub-space X〵 of X such that and is the σ-extension of the canonical Gaussian cylinder measure of a real separable Hilbert space such that the norm is contiunous on and 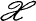is dense in The main purpose of this note is to prove that ‖ • ‖ x〵 is measurable (and not merely continuous) on .

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 46 , March 1972 , pp. 155 - 160
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1972

Footnotes

*

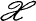This research was partially supported by the NSF under Grant GU-2059.

References

[1] Anderson, T. W., The integral of a symmetric unimodal function over a symmetric convex set and some probability inequalities, Proc. Amer. Math. Soc., 6 (1955), pp. 170–176.CrossRefGoogle Scholar
[2] Dudley, R.M., J. Feldman, L. LeCam, On seminorms and probabilities, and abstract Wiener spaces, (preprint).Google Scholar
[3] Gross, L., Integration and nonlinear transformations in Hilbert space., Trans. Amer. Math. Soc., 94 (1960), pp. 404–440.CrossRefGoogle Scholar
[4] Gross, L., Measurable functions on Hilbert space, Trans. Amer. Math. Soc., 105 (1962), pp. 372–390.Google Scholar
[5] Gross, L., Abstract Wiener spaces, Proceedings of the Fifth Berkeley Symposium, University of California Press, Berkeley, California, Vol. 2, part 1, (1965), pp. 31–42.Google Scholar
[6] Sato, H., Gaussian measure on a Banach space and abstract Wiener measure, Nagoya Math. J., 36 (1969), pp. 65–81.Google Scholar