Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T23:03:31.013Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Covering Surface over an Abstract Riemann Surface

Published online by Cambridge University Press:  22 January 2016

Makoto Ohtsuka
Makoto Ohtsuka*
Affiliation:
Mathematical Institute, Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

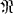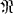1. Let be an abstract Riemann surface in the sense of Weyl-Radó, and an open covering surface over . If a curve C = {P(t);0≦t<1} on tends to the ideal boundary of 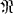but its projection terminates at an inner point of as t→1, we shall say that C determines an accessible boundary point (which will be abbreviated by A.B.P.) of 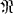relatively to 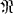. 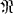The set of all the A.B.P.S of relative to will be called accessible boundary (relative to ) and denoted by 3i() or by 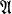(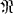, ). Throughout in this paper 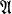(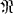) will be supposed to be non-empty.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 4 , June 1952 , pp. 109 - 118
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1952

References

[1] Carathéodory, C.: Elementare Beweis für den Fundamentalsatz der konformen Abbildung, Schwarz Festschrift, Berlin (1914), pp. 19–41.Google Scholar
[2] Frostman, O.: Potentiel d’équilibre et capacité des ensembles avec quelques applications à la théorie des fonctions, Meddel. Lunds. Univ. Mat. Sem., 3 (1935), pp. 1–118.Google Scholar
[3] Lusin, N. and Priwaloff, J.: Sur l’unicité et la multiplicité des fonctions analytiques, Ann. École Norm., 42 (1925), pp. 143–191.CrossRefGoogle Scholar
[4] Mori, A.: On Riemann surfaces, on which no bounded harmonie function exists, which will appear in Journ. Math. Soc. Japan.Google Scholar
[5] Nagai, Y.: On the behaviour of the boundary of Riemann surfaces, II, Proc. Japan Acad., 26 (1950), pp. 10–16 (of No. 6).CrossRefGoogle Scholar
[6] Nevanlinna, R.: Eindeutige analytische Funktionen, Berlin (1936).CrossRefGoogle Scholar
[7] Ohtsuka, M.: Dirichlet problems on Riemann surfaces and conformai mappings, Nagoya Math. Journ., 3 (1951), pp. 91–137.CrossRefGoogle Scholar
[8] Riesz, F.: Über die Randwerte einer analytischen Funktion, Math. Z., 18 (1923), pp. 87–95.CrossRefGoogle Scholar
[9] , F. and Riesz, M.: Über die Randwerte einer analytischen Funktion, 4 Congrès Scand. Stockholm, (1916), pp. 27–44.Google Scholar
[10] Tsuji, M.: Theory of meromorphic function in a neighbourhood of a closed set of capacity zero, Jap. J. Math., 19 (1944), pp. 139–154.CrossRefGoogle Scholar
[11] Tsuji, M.: Some metrical theorems on Fuchsian groups, Kõdai Math. Sem. Report, Nos. 4–5 (1950), pp. 89–93.Google Scholar
[12] Virtanen, K. I.: Über die Existenz von beschränkten harmonischen Funktionen auf offenen Riemannschen Flächen, Ann. Acad. Sci. Fenn., A. I., (1950), No. 75, 7 pp.Google Scholar