Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gustafson, William H.
1981.
Integral Representations and Applications.
Vol. 882,
Issue. ,
p.
1.
Thévenaz, Jacques
1991.
Defect theory for maximal ideals and simple functors.
Journal of Algebra,
Vol. 140,
Issue. 2,
p.
426.


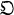 of all integers in
of all integers in 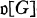 -module.
-module.