Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Itô, Masayuki
1971.
Une caractérisation du principe du balayage pour un espace fonctionnel régulier.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 47,
Issue. S1,
Itô, Masayuki
1971.
Sur le balayage relatif aux noyaux composés.
Hiroshima Mathematical Journal,
Vol. 1,
Issue. 2,
ITO, Masayuki
1971.
Une caractérisation du principe du balayage pour un espace fonctionnel régulier.
Proceedings of the Japan Academy,
Vol. 47,
Issue. SupplementI,
p.
840.
Itô, Masayuki
1973.
Sur le Principe de Domination Pour les Noyaux de Convolution.
Nagoya Mathematical Journal,
Vol. 50,
Issue. ,
p.
149.
Higuchi, Isao
and
Itô, Masayuki
1973.
Characterization of Relative Domination Principle.
Nagoya Mathematical Journal,
Vol. 50,
Issue. ,
p.
175.
Itô, Masayuki
1973.
Noyaux Réguliers et Noyaux Singuliers.
Nagoya Mathematical Journal,
Vol. 50,
Issue. ,
p.
117.
ITÔ, Masayuki
1975.
Une caractérisation du principe de domination pour les noyaux de convolution.
Japanese journal of mathematics. New series,
Vol. 1,
Issue. 1,
p.
5.
1978.
Journal of the Japan Society of Colour Material,
Vol. 51,
Issue. 3,
p.
195.
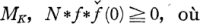
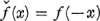 et la signe * est la convolution sur X.
et la signe * est la convolution sur X.