Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Khoshnevisan, Davar
Levin, David A.
and
Méndez-Hernández, Pedro J.
2008.
Capacities in Wiener space, quasi-sure lower functions, and Kolmogorov’s ε-entropy.
Stochastic Processes and their Applications,
Vol. 118,
Issue. 10,
p.
1723.


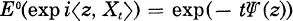 .
.