Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-24T00:20:56.727Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on certain permutation groups in the infinite dimensional rotation group

Published online by Cambridge University Press:  22 January 2016

Nobuaki Obata
Nobuaki Obata*
Affiliation:
Department of Mathematics, Faculty of Science, Nagoya University, Chikusa-ku, Nagoya, 464, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

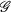In his book P. Lévy discussed certain permutation groups of natural numbers in connection with the theory of functional analysis. Among them the group , called the Lévy group after T. Hida, has been studied along with Hida’s theory of white noise analysis and has become very important keeping profound contact with the Lévy Laplacian which is an infinite dimensional analogue of the ordinary Laplacian.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 109 , March 1988 , pp. 91 - 107
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1988

References

[1] Hida, T., Brownian motion, Applications of Mathematics 11, Springer-Verlag, 1980.Google Scholar
[1] Hida, T., Brownian motion and its functionals, Ricerche Mat., 34 (1985), 183–222.Google Scholar
[1] Hida, T., Analysis of Brownian functionals, Lecture Notes, IMA, University of Minnesota, 1986.Google Scholar
[1] Hida, T., Kubo, I., Nomoto, H. and Yoshizawa, H., On projective invariance of Brownian motion, Publ. RIMS Kyoto Univ., ser. A, 4 (1969), 595–609.CrossRefGoogle Scholar
[1] Hida, T., Lee, K.-S. and Lee, S.-S., Conformal invariance of white noise, Nagoya Math. J., 98 (1985), 87–98.Google Scholar
[1] Hida, T. and Saitô, K., White noise analysis and the Levy Laplacian, to appear in Proc. BiBoS IV (1986).Google Scholar
[1] Kubo, I. and Takenaka, S., Calculus on Gaussian white noise IV, Proc. Japan Acad., 58 ser. A (1982), 186–189.Google Scholar
[1] Levy, P., Problèmes concrets d’analyse fonctionnelle, Part 3, Gauthier-Villars, Paris, 1951.Google Scholar
[1] Saitô, K., Itô’s formula and Lévy Laplacian, Nagoya Math. J., 108 (1987), 67–76.Google Scholar
[10] Yamasaki, Y., Measures on infinite dimensional spaces, Series in Pure Mathematics Vol. 5, World Scientific, 1985.Google Scholar
[11] Yoshizawa, H., Rotation group of Hilbert space and its application to Brownian motion, Proceedings of the International Conference on Functional Analysis and Related Topics, Tokyo, 1969, 414–423.Google Scholar
[12] Zygmund, A., Trigonometric series I, Chapter III, Oxford Univ. Press 1959.Google Scholar