Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T20:12:26.537Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on Blocks of Symmetric Groups

Published online by Cambridge University Press:  22 January 2016

Tadasi Nakayama  and
Masaru Osima
Tadasi Nakayama
Affiliation:
Mathematical Institutes, Nagoya University, Okayama University
Masaru Osima
Affiliation:
Mathematical Institutes, Nagoya University, Okayama University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A conjecture concerning characterization of blocks of representations of symmetric groups by means of Young diagrams, given formerly by one of the writers, was affirmed recently by R. Brauer and G. de B. Robinson jointly. Namely, it was proved in Brauer’s paper, relying on his general, and profound, theory of blocks in finite groups, that the number of p-blocks in a symmetric group 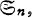of degree n, is exactly equal to the number of p-cores, or p-kernels in the terminology of NI, with n- Ip (l= 0, 1, 2,…) nodes, and that certain statements designated as (A), (B) and (C) would secure that two irreducible representations with a same p-core belong to a same block (whence the conjecture itself when combined with the estimate of the number of blocks). Then these statements (A), (B), (C) were proved actually in Robinson’s paper.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 2 , February 1951 , pp. 111 - 117
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1951

References

1) Nakayama, T., On some modular properties of irreducible representations of symmetric groups I, II, Jap. J. Math. 17 (1941)Google Scholar; we refer to these papers as NI and NIL.

2) Brauer, R., On a conjecture by Nakayama; Robinson, G. de B., On a conjecture by Nakayama, Trans. Roy. Soc. Canada, 41 (1947)Google Scholar.

3) Terms core and node, in place of kernel and Jetter, are after Robinson.

4) The first weak .assertion was shown by the former of the writers and the second was proved by the latter writer by combining his detailed structural analysis of diagrams with the former’s argument for the first assertion.

5) Or, combined with Brauer’s theory of blocks directly; see the end of the present note.

6) For the notions of hooks and cores (kernels), and for their theory, see NI.

7) NI, Appendix. See also Robinson, G. de B., On the representations of the symmetric group, II, Amer. J. Math. 69 (1947); III, 70 (1948)Google Scholar.

8) That p is a prime we use only in congruences (and for the sake of our purpose). As to the structure of diagrams, p need not be a prime in the following considerations.

9) NI.

10) We give this assertion first, since it already has some bearing by itself, as was observed in the introduction, though rather weak, and moreover its proof may be regarded as a model of that of the stronger one in §2.

11) Robinson, l.c. 7) III.

12) Nil, §3.

13) L.c. 7)A skew diagram is a diagram minus a top left partial diagram.

14) Or, more generally, if Po has order divisible by p.

15) The theory is summarized in Brauer I.c. 2). If P′ is an element of possessing lp cycles of length 1 and P 0 is obtained from by removing those lp cycles and if normalizer of P 0 in has an order prime to p, then we can show from (11)