Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T23:47:16.975Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on a Conjecture of Brauer

Published online by Cambridge University Press:  22 January 2016

Paul Fong
Paul Fong*
Affiliation:
University of California, Berkeley 4, California
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [1] R. Brauer asked the following question: Let 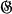be a finite group, p a rational prime number, and B a p-block of 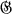with defect d and defect group 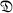. Is it true that 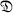is abelian if and only if every irreducible character in B has height 0 ? The present results on this problem are quite incomplete. If d-0, 1, 2 the conjecture was proved by Brauer and Feit, [4] Theorem 2. They also showed that if 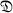is cyclic, then no characters of positive height appear in B. If is normal in 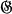, the conjecture was proved by W. Reynolds and M. Suzuki, [12]. In this paper we shall show that for a solvable group 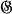, the conjecture is true for the largest prime divisor p of the order of 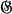. Actually, one half of this has already been proved in [7]. There it was shown that if 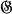is a p-solvable group, where p is any prime, and if 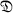is abelian, then the condition on the irreducible characters in B is satisfied.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 22 , June 1963 , pp. 1 - 13
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1963

References

[1] Brauer, R., Number theoretical investigations on groups of finite order, Proceedings of the International Symposium on Algebraic Number Theory, Tokyo, 1956, pp. 55–62.Google Scholar
[2] Brauer, R., On groups whose order contains a prime number to the first power, I, Amer. J. Math, vol 64 (1942), pp. 401–420.CrossRefGoogle Scholar
[3] Brauer, R., Zur Darstellungstheorie der Gruppen endlicher Ordnung I, Math. Z. vol. 63 (1956), pp. 409–444.Google Scholar
[4] Brauer, R. and Feit, W., On the number of irreducible characters of finite groups in a given block, Proc. Nat. Acad. Sci. vol. 45 (1959), pp. 361–365.CrossRefGoogle Scholar
[5] Clifford, A. H., Representations induced in an invariant subgroup, Ann. of Math. vol. 38 (1937), pp. 533–550.Google Scholar
[6] Dickson, L. E., Determination of all the subgroups of the known simple group of order 25920, Trans. A.M.S. vol. 5 (1904), pp. 126–166.CrossRefGoogle Scholar
[7] Fong, P., On the characters of p-solvable groups, Trans. A.M.S. vol. 98 (1961), pp. 263–284.Google Scholar
[8] Hall, P., A contribution to the theory of groups of prime-power order, Proc. London Math. Soc. vol. 36 (1934), pp. 29–95.Google Scholar
[9] Hall, P. and Higman, G., On the p-length of p-soluble groups, Proc. London Math. Soc. vol 6 (1956), pp. 1–42.Google Scholar
[10] Huppert, B., Lineare auflösbare Gruppen, Math. Z. vol. 67 (1957), pp. 479–518.Google Scholar
[11] Huppert, B., Zweifach transitive, auflösbare Permutations-gruppen, Math. Z. vol. 68 (1957), pp. 126–150.Google Scholar
[12] Reynolds, W., Blocks with normal defect group, Seminar on Finite Groups at Harvard University, 1960–1961 (mimeographed notes).Google Scholar