Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T23:26:21.897Z Has data issue: false hasContentIssue false
  • English
  • Français

Normality, Quasinormality and Periodic Points

Published online by Cambridge University Press:  11 January 2016

Jianming Chang
Jianming Chang*
Affiliation:
Department of MathematicsChangshu Institute of Technology, Changshu, Jiangsu 215500, P. R. [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let M > 1 be a positive number. Let 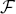be a family of holomorphic functions f in some domain D ⊂ ℂ for which there exists an integer k = k(f) > 2 such that |(fk)′(ζ)| ≤ Mk for every periodic point ζ of period k of f in D. We show first that 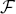is quasinormal of order at most one in D. This strengthens a result of W. Bergweiler. Secondly, for the case M = 1, we prove that 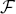is normal in D if there exists a positive number K < 3 such that | f(η)| ≤ K for each f ∈ 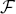and every fixed point η of f in D. This improves a result of M. Esséen and S. J. Wu. We also construct an example which shows that the condition |f’(η)| ≤ K < 3 can not be replaced by | f′(η) | < 3.

Keywords

30D4530D0537F1037C25
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 195 , 2009 , pp. 77 - 95
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2009

References

[1] Baker, I. N., Fix-points of polynomials and rational functions, J. London Math. Soc. (2), 39 (1964), 615–622.Google Scholar
[2] Baker, I. N., Repulsive fixpoints of entire functions, Math. Z., 104 (1968), 252–256.CrossRefGoogle Scholar
[3] Bargmann, D. and Bergweiler, W., Periodic points and normal families, Proc. Amer. Math. Soc., 129 (2001), 2881–2888.CrossRefGoogle Scholar
[4] Bergweiler, W., Periodische Punkte bei der Iteration ganzer Funktionen, Habilitationsschrift, Rheinisch-Westf¨alische Techn. Hochsch., Aachen, 1991.Google Scholar
[5] Bergweiler, W., Periodic points of entire functions: proof of a conjecture of Baker, Complex Variables Theory Appl., 17 (1991), 57–72.Google Scholar
[6] Bergweiler, W., A new proof of the Ahlfors five islands theorem, J. Analyse Math., 76 (1998), 337–347.Google Scholar
[7] Bergweiler, W., Quasinormal families and periodic points, Contemp. Math., 382 (2005), 55–63.Google Scholar
[8] Bergweiler, W., Bloch’s principle, Comput. Methods Funct. Theory, 6 (2006), 77–108.CrossRefGoogle Scholar
[9] Carleson, L. and Gamelin, T. W., Complex Dynamics, Springer, New York, Berlin, Heidelberg, 1993.Google Scholar
[10] Chang, J. M., Polynomials without repelling periodic points of given period, J. Math. Anal. Appl. (1), 324 (2006), 1–13.Google Scholar
[11] Chang, J. M. and Fang, M. L., Normal families and fixed points, J. Analyse Math., 95 (2005), 389–395.Google Scholar
[12] Douady, A. and Hubbard, J. H., On the dynamics of polynomial-like mappings, Ann. ´ Sci. École Norm. Sup. (4), 18 (1985), 287–343.Google Scholar
[13] Essén, M. and Wu, S. J., Fixpoints and normal families of analytic functions, Complex Variables, 37 (1998), 171–178.Google Scholar
[14] Essén, M. and Wu, S. J., Repulsive fixpoints of analytic functions with application to complex dynamics, J. London Math. Soc. (2) 62 (2000), 139–148.Google Scholar
[15] Hayman, W. K., Meromorphic Functions, Clarendon Press, Oxford, 1964.Google Scholar
[16] Hayman, W. K., Research problems in function theory, Athlone Press, London, 1967.Google Scholar
[17] Pang, X. C., Shared values and normal families, Analysis, 22 (2002), 175–182.Google Scholar
[18] Pang, X. C. and Zalcman, L., Normal families and shared values, Bull. London Math. Soc., 32 (2000), 325–331.Google Scholar
[19] Schiff, J., Normal Families, Springer-Verlag, 1993.CrossRefGoogle Scholar
[20] Yang, L., Some recent results and problems in the theory of value distribution, Proc. of the Symposium on Value Distribution Theory in Several Complex Variables (W. Stoll, ed.), University of Notre Dame Press, 1992, pp. 157–171.Google Scholar
[21] Yang, L., Value Distribution Theory, Springer-Verlag, Berlin, 1993.Google Scholar