Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T23:04:25.865Z Has data issue: false hasContentIssue false
  • English
  • Français

A norm residue map for central extensions of an algebraic number field

Published online by Cambridge University Press:  22 January 2016

Yoshiomi Furuta
Yoshiomi Furuta*
Affiliation:
Department of Mathematics, Kanazawa University, Marunouchi, Kanazawa 920, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let K be a finite Galois extension of an algebraic number field k with G = Gal (K/k), and M be a Galois extension of k containing K. We denote by 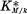resp. 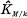the genus field resp. the central class field of K with respect to M/k. By definition, the field 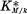is the composite of K and the maximal abelian extension over k contained in M. The field 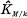is the maximal Galois extension of k contained in M satisfying the condition that the Galois group over K is contained in the center of that over k. Then it is well known that Gal 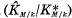is isomorphic to a factor group of the Schur multiplicator H-3(G, Z), and is isomorphic to H-3(G, Z) when M is sufficiently large. In this case we call M abundant for K/k (See Heider [3, § 4] and Miyake [6, Theorem 5]).

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 93 , March 1984 , pp. 61 - 69
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1984

References

[ 1 ] Furuta, Y., Note on class number factors and prime decompositions, N.agoya Math. J., 66 (1977), 167–182.Google Scholar
[ 2 ] Furuta, Y., A prime decomposition symbol for a non-abelian central extension which is abelian over a bicyclic biquadratic field, Nagoya Math. J., 79 (1980), 79–109.Google Scholar
[ 3 ] Heider, F.-P., Strahlkonten und Geschlechterkörper mod m, J. reine angew. Math., 320 (1980), 52–67.Google Scholar
[ 4 ] Kuz’min, L. V., Homology of profinite groups, Schur multipliers, and class field theory, Math. USSR-Izv., 3 (1969), 1149–1181.Google Scholar
[ 5 ] Lyndon, R. G., The cohomology theory of group extensions, Duke Math. J., 15 (1948), 271–292.Google Scholar
[ 6 ] Miyake, K., Central extensions and Schur’s multiplicators of Galois groups, Nagoya Math. J., 90 (1983), 137–144.CrossRefGoogle Scholar
[ 7 ] Razar, M., Central and genus class fields and the Hasse norm theorem, Coripositio Math., 35 (1977), 281–298.Google Scholar