Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-02-11T02:17:36.594Z Has data issue: false hasContentIssue false
  • English
  • Français

NON-LOG LIFTABLE LOG DEL PEZZO SURFACES OF RANK ONE IN CHARACTERISTIC FIVE

Part of: Arithmetic problems. Diophantine geometry Surfaces and higher-dimensional varieties Families, fibrations

Published online by Cambridge University Press:  10 February 2025

MASARU NAGAOKA Open the ORCID record for MASARU NAGAOKA [Opens in a new window]
MASARU NAGAOKA*
Affiliation:
Department of Mathematics Gakushuin University 1-5-1 Mejiro, Toshima-ku, Tokyo 171-8588 Japan
*
[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Building upon the classification by Lacini, we determine the isomorphism classes of log del Pezzo surfaces of rank one over an algebraically closed field of characteristic five either which are not log liftable over the ring of Witt vectors or whose singularities are not feasible in characteristic zero. We also show that such a surface is always constructed from the Du Val del Pezzo surface of Dynkin type 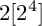$2[2^4]$. Furthermore, We show that the Kawamata–Viehweg vanishing theorem for ample 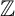$\mathbb {Z}$-Weil divisors holds for log del Pezzo surfaces of rank one in characteristic five if those singularities are feasible in characteristic zero.

Keywords

log del Pezzo surfacesliftability to the ring of Witt vectorspositive characteristic

MSC classification

Primary: 14J26: Rational and ruled surfaces 14D15: Formal methods; deformations
Secondary: 14G17: Positive characteristic ground fields 14J45: Fano varieties
Type
Article
Information
Nagoya Mathematical Journal , First View , pp. 1 - 24
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arvidsson, E., Bernasconi, F. and Lacini, J.. On the Kawamata–Viehweg vanishing theorem for log del Pezzo surfaces in positive characteristic , Compos. Math. 158 (2022), no. 4, 750–763.CrossRefGoogle Scholar
Bădescu, L., Algebraic surfaces, Universitext, Springer-Verlag, New York, 2001. Translated from the 1981 Romanian original by Vladimir Maşek and revised by the author.CrossRefGoogle Scholar
Beauville, A., Les familles stables de courbes elliptiques sur P1 admettant quatre fibres singulières , C. R. Acad. Sci. Paris Sér. I Math. 294 (1982), no. 19, 657–660.Google Scholar
Belousov, G., The maximal number of singular points on log del Pezzo surfaces , J. Math. Sci. Univ. Tokyo. 16 2009, no. (2), 231–238.Google Scholar
Cascini, P. and Tanaka, H., Smooth rational surfaces violating Kawamata-Viehweg vanishing , Eur. J. Math. 4 (2018), no. 1, 162–176.CrossRefGoogle Scholar
Cascini, P. and Tanaka, H., Purely log terminal threefolds with non-normal centres in characteristic two , Amer. J. Math. 141 (2019), no. 4, 941–979.CrossRefGoogle Scholar
Fantechi, B., Göttsche, L., Illusie, L., Kleiman, S. L., Nitsure, N. and Vistoli, A., Fundamental algebraic geometry, Mathematical Surveys and Monographs, Vol. 123, American Mathematical Society, Providence, RI, 2005. Grothendieck’s FGA explained.Google Scholar
Kawakami, T., On Kawamata-Viehweg type vanishing for three dimensional Mori fiber spaces in positive characteristic , Trans. Amer. Math. Soc. 374 (2021), no. 8, 5697–5717.CrossRefGoogle Scholar
Kawakami, T., Bogomolov-Sommese vanishing and liftability for surface pairs in positive characteristic , Adv. Math. 409 (2022), 108640, 35.CrossRefGoogle Scholar
Keel, S. and McKernan, J., Rational curves on quasi-projective surfaces , Mem. Amer. Math. Soc. 140 (1999), no. 669, viii+153.Google Scholar
Kawakami, T. and Nagaoka, M., Pathologies and liftability of Du Val del Pezzo surfaces in positive characteristic , Mathematische Zeitschrift 301 (2022), 1–43.CrossRefGoogle Scholar
Kawakami, T. and Nagaoka, M., Classification of Du Val del Pezzo surfaces of Picard rank one in characteristic two and three , J. Algebra 636 (2023), 603–625.CrossRefGoogle Scholar
Kollár, J., editor, Flips and abundance for algebraic threefolds—A summer seminar at the University of Utah (Salt Lake City, 1991), Astérisque, Vol. 211, Société mathématique de France, Paris, 1992.Google Scholar
Lacini, J., On rank one log del Pezzo surfaces in characteristic different from two and three , Adv. Math. 442 (2024), 109568, 77.CrossRefGoogle Scholar
Lang, W. E., Extremal rational elliptic surfaces in characteristic $p$ . II. Surfaces with three or fewer singular fibres , Ark. Mat. 32 (1994), no. 2, 423–448.CrossRefGoogle Scholar
Langer, A., The Bogomolov-Miyaoka-Yau inequality for logarithmic surfaces in positive characteristic . Duke Math. J. 165 (2016), no. 14, 2737–2769.CrossRefGoogle Scholar
Langer, A., Birational geometry of compactifications of Drinfeld half-spaces over a finite field , Adv. Math. 345 (2019), 861–908.CrossRefGoogle Scholar
Lee, W., Park, E., and Schenzel, P., On the classification of non-normal cubic hypersurfaces , J. Pure Appl. Algebra 215 (2011), no. 8, 2034–2042.CrossRefGoogle Scholar
Takamatsu, T. and Yoshikawa, S., Minimal model program for semi-stable threefolds in mixed characteristic , J. Algebraic Geom. 32 (2023), no. 3, 429–476.CrossRefGoogle Scholar
Ye, Q., On Gorenstein log del Pezzo surfaces , Japan. J. Math. (N.S.) 28 (2002), no. 1, 87–136.CrossRefGoogle Scholar