Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T23:54:13.099Z Has data issue: false hasContentIssue false
  • English
  • Français

Nilpotency and triviality of mod p Morita-Mumford classes of mapping class groups of surfaces

Published online by Cambridge University Press:  22 January 2016

Toshiyuki Akita
Toshiyuki Akita*
Affiliation:
Department of Mathematics, Hokkaido University, Sapporo, 060-0810, Japan, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper is concerned with mod p Morita-Mumford classes 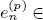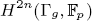of the mapping class group Γg of a closed oriented surface of genus g ≥ 2, especially triviality and nontriviality of them. It is proved that 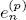is nilpotent if n ≡ − 1 (mod p − 1), while the stable mod p Morita-Mumford class 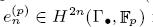is proved to be nontrivial and not nilpotent if n ≢ −1 (mod p − 1). With these results in mind, we conjecture that 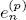vanishes whenever n ≡ − 1 (mod p − 1), and obtain a few pieces of supporting evidence.

Keywords

55R4057R2014H3720J06
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 165 , March 2002 , pp. 1 - 22
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2002

References

[1] Akita, T., Kawazumi, N. and Uemura, T., Periodic surface automorphisms and algebraic independence of Morita-Mumford classes, J. Pure Appl. Algebra, 160 (2001), 1–11.CrossRefGoogle Scholar
[2] Atiyah, M. F., The signature of fibre-bundles, Global Analysis (Papers in Honor of K. Kodaira), Univ. Tokyo Press, Tokyo, 1969, pp. 73–84.Google Scholar
[3] Borevich, A. I. and Shafarevich, I. R., Number theory, Academic Press, New York, 1966.Google Scholar
[4] Brown, K. S., Cohomology of Groups, Springer-Verlag, New York, 1982.Google Scholar
[5] Cohen, F. R., Homology of mapping class groups for surfaces of low genus, The Lefschetz centennial conference, Part II (Mexico City, 1984), Contemp. Math. 58, II, Amer. Math. Soc., Providence (1987), pp. 21–30.Google Scholar
[6] Earle, C. J. and Eells, J., A fibre bundle description of Teichmüller theory, J. Differential Geometry, 3 (1969), 19–43.Google Scholar
[7] Endo, H., A construction of surface bundles over surfaces with non-zero signature, Osaka J. Math., 35 (1998), 915–930.Google Scholar
[8] Faber, C., Chow rings of moduli spaces of curves. I. The Chow ring of , Ann. of Math. (2), 132 (1990), 331–419.Google Scholar
[9] Faber, C. and Looijenga, E. (eds.), Moduli of Curves and Abelian Varieties, The Dutch Intercity Seminar on Moduli, Aspects of Mathematics, E33, Friedr. Vieweg & Sohn, Braunschweig, 1999.Google Scholar
[10] Glover, H. H., Mislin, G. and Xia, Y., On the Yagita invariant of mapping class groups, Topology, 33 (1994), 557–574.Google Scholar
[11] Hain, R. and Looijenga, E., Mapping class groups and moduli spaces of curves, Algebraic geometry-Santa Cruz 1995, Proc. Sympos. Pure Math., 62, Part 2, Amer. Math. Soc., Providence (1997), pp. 97–142.Google Scholar
[12] Harer, J. L., The second homology group of the mapping class group of an orientable surface, Invent. Math., 72 (1983), 221–239.Google Scholar
[13] Harer, J. L., Stability of the homology of the mapping class groups of orientable surfaces, Ann. of Math. (2), 121 (1985), 215–249.CrossRefGoogle Scholar
[14] Harer, J. L., The virtual cohomological dimension of the mapping class group of an orientable surface, Invent. Math., 84 (1986), 157–176.Google Scholar
[15] Harer, J. L., The cohomology of the moduli space of curves, Theory of moduli (Montecatini Terme, 1985), Lecture Notes in Math., 1337, Springer, Berlin (1988), pp. 138–221.Google Scholar
[16] Harer, J. L., The third homology group of the moduli space of curves, Duke Math. J., 63 (1991), 25–55.Google Scholar
[17] Harvey, W. J., Cyclic groups of automorphisms of a compact Riemann surface, Quart. J. Math. Oxford Ser. (2), 17 (1966), 86–97.Google Scholar
[18] Igusa, J.-I., Arithmetic variety of moduli for genus two, Ann. of Math. (2), 72 (1960), 612–649.Google Scholar
[19] Ivanov, N. V., On the homology stability for Teichmüller modular groups: closed surfaces and twisted coefficients, Mapping class groups and moduli spaces of Riemann surfaces (Göttingen, 1991/Seattle, WA, 1991), Contemp. Math., 150, Amer. Math. Soc., Providence (1993), pp. 149–194.Google Scholar
[20] Kawazumi, N., Homology of hyperelliptic mapping class groups for surfaces, Topology Appl., 76 (1997), 203–216.Google Scholar
[21] Kawazumi, N. and Uemura, T., Riemann-Hurwitz formula for Morita-Mumford classes and surface symmetries, Kodai Math. J., 21 (1998), 372–380.Google Scholar
[22] Kerckhoff, S. P., The Nielsen realization problem, Ann. of Math. (2), 117 (1983), 235–265.Google Scholar
[23] Kodaira, K., A certain type of irregular algebraic surfaces, J. Analyse Math., 19 (1967), 207–215.Google Scholar
[24] Lee, R. and Weintraub, S. H., Cohomology of Sp4(Z) and related groups and spaces, Topology, 24 (1985), 391–410.Google Scholar
[25] Looijenga, E., Cohomology of M3 and M1 3, Mapping class groups and moduli spaces of Riemann surfaces (Göttingen, 1991/Seattle, WA, 1991), Contemp. Math., 150, Amer. Math. Soc., Providence (1993), pp. 205–228.Google Scholar
[26] Meyer, W., Die Signatur von Flächenbündeln, Math. Ann., 201 (1973), 239–264.Google Scholar
[27] Miller, E. Y., The homology of the mapping class group, J. Differential Geom., 24 (1986), 1–14.CrossRefGoogle Scholar
[28] Morita, S., Characteristic classes of surface bundles, Invent. Math., 90 (1987), 551–577.Google Scholar
[29] Morita, S., Characteristic classes of surface bundles and bounded cohomology, A fête of topology, Academic Press, Boston (1988), pp. 233–257.CrossRefGoogle Scholar
[30] Morita, S., Mapping class groups of surfaces and three-dimensional manifolds, Proceedings of the International Congress of Mathematicians, Vol. I, II (Kyoto, 1990), Math. Soc. Japan, Tokyo (1991), pp. 665–674.Google Scholar
[31] Morita, S., The structure of the mapping class group and characteristic classes of surface bundles, Mapping class groups and moduli spaces of Riemann surfaces (Göttingen, 1991/Seattle, WA, 1991), Contemp. Math., 150, Amer. Math. Soc., Providence (1993), pp. 303–315.Google Scholar
[32] Morita, S., Characteristic classes of surface bundles and the Casson invariant, Sugaku Expositions, 7 (1994), 59–79.Google Scholar
[33] Morita, S., Problems on the structure of the mapping class group of surfaces and the topology of the moduli space of curves, Topology, geometry and field theory, World Sci. Publishing, River Edge (1994), pp. 101–110.Google Scholar
[34] Morita, S., Structure of the mapping class groups of surfaces: a survey and a prospect, Proceedings of the Kirbyfest (Berkeley, CA, 1998), Geometry & Topology Monographs 2, Geometry & Topology, Coventry (1999), 349–406.Google Scholar
[35] Mumford, D., Towards an enumerative geometry of the moduli space of curves, Arithmetic and geometry, Vol. II, Progr. Math., 36, Birkhäuser Boston, Boston (1983), pp. 271–328.Google Scholar
[36] Quillen, D., The spectrum of an equivariant cohomology ring. II, Ann. of Math. (2), 94 (1971), 573–602.Google Scholar
[37] Symonds, P., The cohomology representation of an action of Cp on a surface, Trans. Amer. Math. Soc., 306 (1988), 389–400.Google Scholar
[38] Uemura, T., Morita-Mumford classes on finite cyclic subgroups of the mapping class group of closed surfaces, Hokkaido Math. J., 28 (1999), 597–611.Google Scholar
[39] Xia, Y., The p-torsion of the Farrell-Tate cohomology of the mapping class group Γ(p-1)/2, Topology ‘90 (Columbus, OH, 1990), Ohio State Univ. Math. Res. Inst. Publ., 1, de Gruyter, Berlin (1992), pp. 391–398.Google Scholar