Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-06T01:23:07.086Z Has data issue: false hasContentIssue false
  • English
  • Français

Newforms of half-integral weight

Published online by Cambridge University Press:  22 January 2016

Thomas R. Shemanske
Thomas R. Shemanske*
Affiliation:
Department of Mathematics, 6188 Bradley Hall, Dartmouth College, Hanover, New Hampshire 03755-3551, U.S.A., E-mail address: [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Two very different definitions of a newform of half-integral weight are present and continued to be developed in the literature. The first definition originated with Serre and Stark for forms of weight 1/2 [5], and is analogous to the definition of newform for integral weight forms, which uses forms of lower level and shifts of such forms 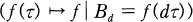to characterize the notion of old-forms. The second definition originated with Kohnen for half-integral weight forms of squarefree level [1], who used forms of lower level and their image under the Um2 operator 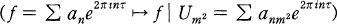to define the notion of oldforms. The choice of the Um2 operator over the shift operator Bd seems a propitious one, since the U operator commutes with the action of the Shimura lift, while the shift operator B does not. More to the point, Kohnen was able to develop a newform theory on a distinguished subspace of the full space of cusp forms (now referred to as the Kohnen subspace), and obtained a multiplicity-one result (with respect to Hecke eigenvalues) for half-integral weight newforms in this subspace. Even nicer, the multiplicity-one result was established by showing that there is a one-to-one correspondence between newforms of level AN in the subspace and the newforms of integral weight of level N.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 143 , September 1996 , pp. 147 - 169
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1996

References

[ 1 ] Kohnen, W., Newforms of half-integral weight, J. reine angew. Math., 333 (1982), 32–72.Google Scholar
[ 2 ] Li, W., Newforms and functional equations, Math. Annalen, 212 (1975), 285–315.Google Scholar
[ 3 ] Manickam, M., Ramakrishnan, B., Vasudevan, T., On the theory of newforms of half-integral weight, J. Number Theory, 34 (1990), 210–224.Google Scholar
[ 4 ] Niwa, S., On Shimura’s trace formula, Nagoya Math J., 66 (1977),183–202.Google Scholar
[ 5 ] Serre, J.-P. and Stark, H., Modular forms of weight 1/2, In Lecture Notes in Math. 627, Springer-Verlag, Berlin and New York (1977), 27–67.Google Scholar
[ 6 ] Shemanske, T., Cuspidal newforms and chracter twists, J. reine angew. Math., 328 (1981), 59–71.Google Scholar
[ 7 ] Shemanske, T. and Walling, L., Determining multiplicities of half-integral weight newforms, Pacific J. Math., 167 (1995), 345–383.Google Scholar
[ 8 ] Shimura, G., On modular forms of half-integral weight, Annals of Math., 97 (1973), 440–481.Google Scholar
[ 9 ] Shimura, G., The critical values of certain zeta functions associated with modular forms of half-integral weight, J. Math. Soc. Japan, 33 (1981), 649–672.Google Scholar
[10] Ueda, M., The decomposition of the spaces of cusp forms of half-integral weight and the trace formula of Hecke operators, J. Math. Kyoto U., 28 (1988), 505–555.Google Scholar
[11] Ueda, M., The trace formula of twisting operators on the spaces of cusp forms of half-integral weight and some trace relations, Japanese J. Math., 17 (1991), 83–135.Google Scholar
[12] Ueda, M., On twisting operators and newforms of half-integral weight, Nagoya Math J., 131 (1993), 135–205.Google Scholar