Hostname: page-component-7479d7b7d-pfhbr Total loading time: 0 Render date: 2024-07-08T12:40:24.014Z Has data issue: false hasContentIssue false
  • English
  • Français

Multipliers on vector spaces of holomorphic functions

Published online by Cambridge University Press:  22 January 2016

Hermann Render  and
Andreas Sauer
Hermann Render
Affiliation:
Universitat Duisburg, Fachbereich Mathematik, Lotharstr. 65, D-47057 Duisburg Federal, Republic of Germany, [email protected]
Andreas Sauer
Affiliation:
Universitat Duisburg, Fachbereich Mathematik, Lotharstr. 65, D-47057 Duisburg Federal, Republic of Germany, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a domain in the complex plane containing zero and H(G) be the set of all holomorphic functions on G. In this paper the algebra M(H(G)) of all coefficient multipliers with respect to the Hadamard product is studied. Central for the investigation is the domain 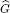introduced by Arakelyan which is by definition the union of all sets 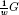with w ∈ Gc. The main result is the description of all isomorphisms between these multipliers algebras. As a consequence one obtains: If two multiplier algebras M(H(G1)) and M(H(G2)) are isomorphic then 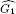is equal to 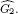Two algebras H(G1) and H(G2) are isomorphic with respect to the Hadamard product if and only if G1 is equal to G2. Further the following uniqueness theorem is proved: If G1 is a domain containing 0 and if M(H(G)) is isomorphic to H(G1) then G1 is equal to .

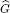Type
Research Article
Information
Nagoya Mathematical Journal , Volume 159 , 2000 , pp. 167 - 178
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2000

References

[1] Arakelyan, N.U., On efficient analytic continuation of power series, Math. USSR Sbornik, 52 (1985), 21–39.Google Scholar
[2] Duren, P.L., Univalent functions, Springer, Berlin-Heidelberg-New York, 1983.Google Scholar
[3] Husain, T., Multipliers of topological algebras, Dissertationes Math., 285, Warzawa 1989.Google Scholar
[4] Larsen, R., Introduction to the theory of multipliers, Springer, Berlin, 1971.CrossRefGoogle Scholar
[5] Müller, J., The Hadamard multiplication theorem and applications in summability theory, Complex variables, 18 (1992), 75–81.Google Scholar
[6] Müller, J., Coefficient multipliers from H(G1) into H(G2), Arch. Math., 61 (1993), 155–166.Google Scholar
[7] Remmert, R., Funktionentheorie II, Springer, Berlin-Heidelberg-New York, 1991.Google Scholar
[8] Render, H., Sauer, A., Algebras of holomorphic functions with Hadamard multiplication, Studia Math., 118 (1996), 77–100.CrossRefGoogle Scholar
[9] Render, H., Sauer, A., Invariance properties of homomorphisms on algebras of holomorphic functions with Hadamard multiplication, Studia Math., 121 (1996), 53–65.Google Scholar
[10] Render, H., Homomorphisms on Hadamard algebras, Rendiconti del Circolo Matematico di Palermo, Serie II, Suppl., 40 (1996), 153–158.Google Scholar
[11] Render, H., Hadamard’s multiplication theorem — Recent Developments, Colloq. Math., 74 (1997), 79–92.Google Scholar
[12] Render, H., Topological algebras with an orthogonal total sequence, Colloq. Math., 72 (1997), 215–221.Google Scholar
[13] Żelazko, W., Banach algebras, Elsevier Publishing Company, Amsterdam, 1973.Google Scholar