Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T23:11:33.991Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiplicity and t-isomultiple ideals

Published online by Cambridge University Press:  22 January 2016

M.E. Rossi  and
G. Valla
M.E. Rossi
Affiliation:
Dipartimento di Matematica, Università di Genova, 16132 Genova, Italy
G. Valla
Affiliation:
Dipartimento di Matematica, Università di Genova, 16132 Genova, Italy
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

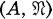Let V be an irreducible non degenerate variety in Pn; a classical geometric result says that degree (V) ≥ codim V + 1 and, if equality holds, V is said to be of minimal degree. Varieties of minimal degree has been classified by Del Pezzo and Bertini and they all are intersections of quadrics. The local version of this result is due to J. Sally who proved that if is a regular local ring and 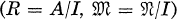is a Cohen-Macaulay local ring of minimal multiplicity, according to the bound e(R) ≥ height (I) + 1 given by Abhyankar, then the tangent cone 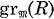of R is intersection of quadrics and it is Cohen-Macaulay.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 110 , June 1988 , pp. 81 - 111
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1988

References

[B] Bourbaki, N., Commutative algebra, Vol. VIII, Addison-Wesley, Reading, Masson Paris (1983).Google Scholar
[Br] Brundu, M., Piattezza normale e isomolteplicità, Rend. Sem. Mat. Univ. Politeen. Torino, Vol. 40, Io (1982), 163–172.Google Scholar
[E] Elias, J., A sharp bound for the minimal number of generators of perfect height two ideals, Man. Math., Vol. 55 Fasc. 1 (1986), 93–99.CrossRefGoogle Scholar
[E-I] Elias, J., Iarrobino, A., The Hilbert function of a Cohen-Macaulay local algebra; extremal Gorenstein algebras, J. Algebra, to appear.Google Scholar
[F-L] Froberg, R., Laksov, D., Compressed algebras, Complete intersections, Acireale (1983), Lect. Notes in Math., 109, 2, Springer (1984), 121–151.Google Scholar
[G] Giusti, M., Some effective problems in Polynomial ideal theory, EUROSAM 1984.Google Scholar
[H-R-V] Herzog, J., Rossi, M. E., Valla, G., On the depth of the Symmetric algebra, Trans. Amer. Math. Soc, 296 (1986), 577–606.CrossRefGoogle Scholar
[H-M] Huneke, C., Miller, M., A note on the multiplicity of Cohen-Macaulay Algebras with pure resolution preprint.Google Scholar
[I] Iarrobino, A., Compressed algebras, Trans. Amer. Math. Soc, 285 (1984), 337–378.CrossRefGoogle Scholar
[K] Kunz, E., Almost complete intersections are not Gorenstein rings, J. Algebra, 23 (1974), 111–115.CrossRefGoogle Scholar
[Me] Macaulay, F. S., The algebraic theory of algebraic systems, Cambridge University (1916).CrossRefGoogle Scholar
[Ma] Maurer, J., Eine variante der Moh-curven, preprint.Google Scholar
[M] Micali, A., Sur les algebres universelles (Thesis), Ann. Inst. Fourier Grenoble, 14 (1964), 33–88.CrossRefGoogle Scholar
[Mo] Moh, T. T., On the unboundness of generators of prime ideals in power series rings of three variables, J. Math. Soc. Japan, 26 (1974), 722–734.Google Scholar
[O] Orecchia, F., Generalized Hilbert functions of Cohen-Macaulay varieties, Algebraic geometry—Open problems, Ravello (1982), Lect. Notes in Math., 997, Springer (1980), 376–390.Google Scholar
[R1] Risler, J. J., Sur la réduction de l’algèbre symétrique de l’idéal maximal d’un anneau local, C. R. Acad. Sci. Paris, t. 266 (1968), Série A, 1177–1179.Google Scholar
[R2] Risler, J. J., Algèbre symétrique d’un idéal, C. R. Acad. Sci. Paris, t. 268 (1969), Série A, 365–368.Google Scholar
[Ro] Robbiano, L., Coni tangenti a singolarità razionali, Atti del Convegno di Geometria Algebrica, Firenze (1981).Google Scholar
[R-V] Robbiano, L., Valla, G., Free resolutions for special tangent cones, Commutative Algebra, Proc. of the Trento Conference, Lect. Notes in Pure and Applied Math. Series 84, Marcel Dekker (1983).Google Scholar
[Sa1] Sally, J. D., On the associated graded ring of a local Cohen-Macaulay ring, J. Math. Kyoto Univ., 17 (1977), 19–21.Google Scholar
[Sa2] Sally, J. D., Cohen-Macaulay Local Rings of Embedding Dimension e + d − 2, J. Algebra, 83 (1983), 393–408.CrossRefGoogle Scholar
[S] Schaub, D., Propriété topologique du gradué associé d’un anneau (Sr ) Comm. Algebra, 5(11), (1977), 1223–1239.CrossRefGoogle Scholar
[Sch] Schenzel, P., Uber die freien Auflosungen extremaler Cohen-Macaulay-Ringe, J. Algebra, 64, No. 1 (1980), 93–101.CrossRefGoogle Scholar
[St] Stanley, R. P., Hilbert Functions of Graded Algebras, Adv. in Math., 28 (1978), 57–83.CrossRefGoogle Scholar
[V-V] Valabrega, P., Valla, G., Form rings and regular sequence, Nagoya Math. J., 72 (1978), 93–101.CrossRefGoogle Scholar