Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T23:06:48.507Z Has data issue: false hasContentIssue false
  • English
  • Français

Mourre theory for time-periodic systems

Published online by Cambridge University Press:  22 January 2016

Koichiro Yokoyama
Koichiro Yokoyama*
Affiliation:
Department of Mathematics, Osaka University, Toyonaka 560-0043, Japan, [email protected]
Rights & Permissions [Opens in a new window]

Abstract.

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

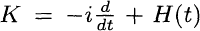Studies for A.C. Stark Hamiltonian are closely related to that for the self-adjoint operator on torus. In this paper we use Mourre’s commutator method, which makes great progress for the study of time-independent Hamiltonian. By use of it we show the asymptotic behavior of the unitary propagator 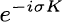as σ → ± ∞.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 149 , March 1998 , pp. 193 - 210
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1998

References

[Gé1] Gérard, C., Sharp propagation estimates for N-particle systems, Duke Math. J., 67 (1992), 483–515.CrossRefGoogle Scholar
[Gé2] Gérard, C., Asymptotic completeness for 3-particle long-range systems, Invent. Math., 114 (1993), 333–397.Google Scholar
[H-S] Helffer, B. and Sjöstrand, J., Equation de Schrödinger avec champ magnétique et équation de Harper, Lecture Notes in Physics, 345, Schrödinger Operators, (1989), Springer, Berlin-Heidelberg-New York, 118–197.Google Scholar
[How] Howland, J., Scattering Theory for Hamiltonians Periodic in Time, Indiana Univ. Math. J., 28 (1979), 471–494.CrossRefGoogle Scholar
[Ka] Kato, T., Wave operators and similarity for some nonselfadjoint operators, Math. Ann., 162 (1966), 258–276.Google Scholar
[Ki-Y] Kitada, H. and K. Yajima, A scattering theory for time-dependent long range potentials, Duke Math. J., 49 (1982), 341–376.Google Scholar
[Ku-Y] Kuwabara, Y. and Yajima, K., The limiting absorption principle for Schrödinger operators with long-range time-periodic potentials, J. Fac. Sci. Univ. Tokyo Sect. IA, Math., 34 (1987), 833–851.Google Scholar
[Mo] Mourre, E., Absence of singular continuous spectrum for certain self-adjoint operators, Commun. Math. Phys., 78 (1981), 391–408.Google Scholar
[Na] Nakamura, S., Asymptotic completeness for three-body Schrödinger equations with time periodic potentials, J. Fac. Sci. Univ. Tokyo Sect. IA, Math., 33 (1986), 379–402.Google Scholar
[PSS] Perry, P., Sigal, I. M. and Simon, B., Spectral analysis of N-bodySchrödinger operators, Ann. Math., 114 (1981), 519–567.Google Scholar
[R-S] Reed, M. and Simon, B., Methods of Modern Mathematical Physics, 1–4, Academic Press, New York-San Francisco-London.Google Scholar
[Sk] Skibsted, E., Propagation estimates for N-body Schrödinger operators, Commun. Math. Phys., 91 (1991), 67–98.Google Scholar
[Ya] Yajima, K., Scattering theory for Schrödinger operators with potentials periodic in time, J. Math. Soc. Jpn., 29 (1977), 729–743.CrossRefGoogle Scholar